Дифракция от параллельных щелей.

Рассмотрим дифракцию параллельного пучка лучей, которые падают нормально к плоскости решетки (см. рис.1)

 

Рис. 1

 

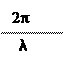Фазы колебаний соответствующих лучей, например 1 и 2, проходят через ближайшие щели, будут, отличаться друг от друга на величину:

 

γ= (a+b)sin φ (5)

 

где а – ширина щели; b – промежуток между щелями.

 

 

Общую напряженность в точке L, которая создается волнами, идущими в направлении φ, можно рассчитать через напряженность отдельных волн E₁, E₂, E_{3, …,} E_n, проходящих сквозь щели

E_φn = E₁ + E₂ + … + E_n (6)

Гдеn– число щелей.

E₁, E₂,…, E_n, могут быть определены из (2)

Векторную сумму можно заменить арифметической, так как направление векторов напряженности одинаковы.

Амплитуды будут равны одной и той же величине E_φ0. Тогда:

E_φ = E_φ0{cos ωt +cos (ωt + j) +… + cos[ωt + (n-1) j ] } (7)

Можно найти сумму, входящую в (7) графическим путем. Получим выражение для амплитуды напряженности эл. поля, которые после дифракции распространяются в направлении φ:

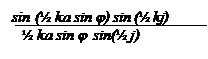E_n0 = E₀² (8)

 

 

Проведем анализ формулы (8).

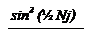1. Распределение потока эл. волн в результате дифракции на решетке определяется произведением двух функций:

sin2(½ j )

E_φ0² = E_o² (9)O² = (10)

 

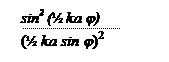
1. Главные минимумы определяются из условия:

a sin φ = mλ , m=0, 1, 2

Это условие справедливо для любого числа щелей.

1. N+1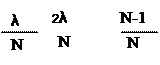

   Главные максимумы определяются из условия:

 

N

sin (½ nj) = 0, т.е. (a+b)sin φ = , , …, λ, λ (13)

 

В результате дифракции поток перераспределяется в основном вблизи направлений, соответствующим главным максимумам.

Различие между <<дифракцией Френеля>> и <<дифракцией Фраунгофера>> представляет собой по существу различие в способах наблюдения дифракции на различного рода оптических неоднородностях (диафрагмах, экранах, преградах, щелях и т. д.)

 

 

 

Пусть дифракция света от источника S происходит на отверстии диаметром D. Если точка наблюдения О выбрана сравнительно близко, (т.е. D/b >> λ/D), то имеет место дифракция Френеля.

Если наблюдать дифракцию в достаточно удаленной точке(D/b << λ/D), то говорят о дифракции Фраунгофера.

Выполнению последнего условия удовлетворят способ наблюдения в параллельных лучах, при котором дифракция наблюдается в фокальной плоскости собирающей линзы, или при помощи зрительной трубы, установленной на бесконечность.

Дифракционная решетка – спектральный прибор. Она представляет собой плоскую прозрачную или отраженную пластинку, на которой нанесены равноотстоящие штрихи. Сумму прозрачных и непрозрачных промежутков называют постоянной решетки: (a+b)=d

 

 

 

Пусть на решетку D падает монохроматический пучок света, в соответствии с принципом Гюйгенса-Френеля, каждая точка внутри любой щели решетки становится источником вторичного поля.

В пространстве за решеткой происходит перераспределение освещенности по законам взаимодействия когерентных источников.

Собирательная линза поставлена затем, чтобы можно было наблюдать дифракцию в её фокальной плоскости на экране Э.

Пусть на решетку падает плоская волна, тогда в плоскости решетки колебания имеют одну фазу. Так как линза не вносит дополнительной разности фаз, то смещение по фазе у лучей прошедших в точку наблюдения от различных точек решетки создается за счет разности хода этих лучей до линзы. Если разность хода лучей δ, исходящих от соответствующих точек соседних щелей составляет целое число к= 0,1,2… длин волн λ, то в данном направлении образуется максимум порядка к.

δ = dsin φ = кλ (*)

Уравнение (*) основное уравнение решетки. Пользуясь им можно определить либо постоянную решетки d, зная λ, либо найти длину световой волны, зная период решетки: к = [d/λ].