Вторая формула Рунге.
Так как модуль и знак апостериорной погрешности из формулы (4) известны, можно уточнить искомое значение 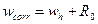 . Это вторая формула Рунге. Однако теперь погрешность wcorr не определена, известно лишь, что она по модулю меньше R0.
. Это вторая формула Рунге. Однако теперь погрешность wcorr не определена, известно лишь, что она по модулю меньше R0.
Алгоритм Эйткена.
Способ оценки погрешности для случая, когда порядок метода p неизвестен. Более того, алгоритм позволяет опытным путем определить и порядок метода. Для этого в третий раз вычислим значение величины w с шагом k2h:
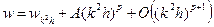 . (5)
. (5)
Приравняем правые части выражений (5) и (3):  . Отсюда:
. Отсюда:
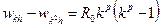 . Подставим сюда значение R0 из (4):
. Подставим сюда значение R0 из (4):
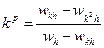 . Из этой формулы определяем знаменатель для (4). Кроме того, определяем порядок
. Из этой формулы определяем знаменатель для (4). Кроме того, определяем порядок 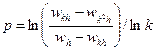 . Для правильно реализованных алгоритмов методов априорных и апостериорных порядки должны получиться совпадающими. Программная реализация формул Рунге позволяет вычислить определенные интегралы с заданной точностью, когда выбор необходимого числа разбиений интервала интегрирования осуществляется автоматически. Пример – уже рассмотренная ранее формула Ромберга.
. Для правильно реализованных алгоритмов методов априорных и апостериорных порядки должны получиться совпадающими. Программная реализация формул Рунге позволяет вычислить определенные интегралы с заданной точностью, когда выбор необходимого числа разбиений интервала интегрирования осуществляется автоматически. Пример – уже рассмотренная ранее формула Ромберга.