ЭЛЕКТРОМАГНЕТИЗМ

 

· Закон Био — Савара — Лапласа

dB [dl,r] ,

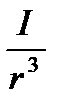где dB — магнитная индукция поля, создаваемого элементом iпроводника с током; m — магнитная проницаемость; m₀ — магнитная постоянная (m₀ =4p · 10 ^-7Гн/м); dl — вектор, равный по модулю длине dlпроводника и совпадающий по направлению с током (элемент проводника); I — сила тока; r — радиус-вектор, проведенный от середины элемента проводника к точке, магнитная индукция в которой определяется.

Модуль вектора dB выражается формулой

dB dl,

где a — угол между векторами dlи r.

· Магнитная индукция В связана с напряженностью Н магнитного поля (в случае однородной, изотропной среды) соотношением

B 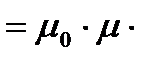H

или в вакууме

B₀=μ₀∙H.

 

· Магнитная индукция в центре кругового проводника с током

В ,

где R — радиус кривизны проводника.

· Магнитная индукция поля, создаваемого бесконечно длинным прямым проводником с током,

В ,

где r — расстояние от оси проводника.

Магнитная индукция поля, создаваемого отрезком проводником

В .

Обозначения ясны из рис.46, а. Вектор индукции В перпенди­кулярен плоскости чертежа, направлен к нам и поэтому изображен точкой.

При симметричном расположении концов проводника относи­тельно точки, в которой определяется магнитная индукция (рис. 46, б), 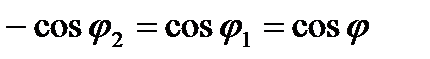и, следовательно,

В

Рис. 46

· Магнитная индукция поля, создаваемого соленоидом в сред­ней его части (или тороида на его оси),

В

где п — число витков, приходящих­ся на единицу длины соленоида;

I— сила тока в одном витке.

· Принцип суперпозиции маг­нитных полей: магнитная индук­ция В результирующего поля равна векторной сумме магнитных индукций В₁,В₂, ...,В_n складываемых полей, т. е.

B В_i.

В частном случае наложения двух полей

В=В₁+В₂,

а модуль магнитной продукции

,

где a — угол между векторами В₁ и В₂.

• Закон Ампера. Сила, действующая на проводник с токомв магнитном поле,

F=[l,B]∙I,

где I— сила тока; l— вектор, равный по модулю длине l проводника и совпадающий по направлению с током; В — магнитная индукция поля.

Модуль вектора F определяется выражением

F=B∙I∙l∙sinα,

где α — угол между векторами l и В.

• Сила взаимодействия двух прямых бесконечно длинных па­раллельных проводников с токами I₁ и I₂, находящихся на расстоянии dдруг от друга, рассчитанная на отрезок проводника длиной lвыражается формулой

.

• Магнитный момент контура с током

p_m=I∙S,

где S — вектор, равный по модулю площади S, охватываемой кон­туром, и совпадающий по направлению с нормалью к его плоскости.

 

• Механический момент, действующий на контур с током, по­мещенный в однородное магнитное поле,

M=[p_m∙B].

Модуль механического момента

M=p_m∙B∙sinα,

где α — угол между векторами р_m и В.

• Потенциальная (механическая) энергия контура с током в магнитном поле

П_мех=p_m∙B =p_m∙B∙cosα.

• Сила, действующая на контур с током в магнитном поле (из­меняющемся вдоль оси x),

,

где —изменение магнитной индукции вдоль оси Ох, рассчи­танное на единицу длины; α — угол между векторами р_m и В.

• Сила F,действующая на заряд Q, движущийся со скоростью υв магнитном поле с индукцией В(сила Лоренца), выражается фор­мулой

F=Q[υ,B] или F=|Q|∙u∙B∙sina,

где a— угол, образованный вектором скорости υдвижущейся ча­стицы и вектором Виндукции магнитного поля.

· Циркуляция вектора магнитной индукции В вдоль замкну­того контура

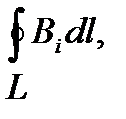
где B_i — проекция вектора магнитной индукции на направление элементарного перемещения dl вдоль контура L. Циркуляция век­тора напряженности Н вдоль замкнутого контура

,

· Закон полного тока (для магнитного поля в вакууме)

где m₀=4∙π∙10^-7Гн/м- магнитная постоянная; - алгебраическая сумма токов, охватываемых контуром; п - число токов.

Закон полного тока (для произвольной среды)

· Магнитный поток Ф через плоский контур площадью S:

а) в случае однородного поля

Ф=B∙S∙cosa; или Ф = B_nS,

где a — угол между вектором нормали n к плоскости контура и век­тором магнитной индукцииВ;В_n — проекция вектора В на нормаль n(B_n=Bcosa);

б) в случае неоднородного поля

где интегрирование ведется во всей поверхности S.

· Потокосцепление, т.е. полный магнитный поток, сцепленный со всеми витками соленоида или тороида,

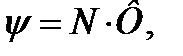
где Ф — магнитный поток через один виток; N — число витков со­леноида или тороида.

· Магнитное поле тороида, сердечник которого составлен из двух частей, изготовлен­ных из веществ с раз­личными магнитными проницаемостями:

а) магнитная индук­ция на осевой линии тороида

где I — сила тока в об­мотке тороида; N — чис­ло ее витков; l₁ и l₂ -­ длины первой и второй частей сердечника торо­ида; m₁и m₂ —магнитные проницаемости ве­ществ первой и второй частей сердечника торо­ида; m₀—магнитная постоянная

б) напряженность магнитного поля на осе­вой линии тороида в первой и второй частях сердечника

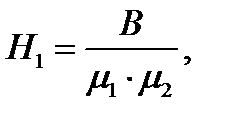
в) магнитный поток в сердечнике тороида

или по аналогии с законом Ома (формула Гопкинсона)

Ф_m=F_m/R_m,

где F_m- магнитодвижущая сила;R_m- полное магнитное сопро­тивление цепи;

г) магнитное сопротивление участка цепи

R_m=l/(μ∙μ₀S).

• Магнитная проницаемостьμ, ферромагнетика связана с маг­нитной индукцией В поля в нем и напряженностью Н намагничи­вающего поля соотношением

μ=B/(μ₀H).

• Работа по перемещению замкнутого контура с током в маг­нитном поле

A=I∙DФ,

где DФ — изменение магнитного потока, пронизывающего поверх­ность, ограниченную контуром; I — сила тока в контуре.

• Основной закон электромагнитной индукции (закон Фарадея — Максвелла)

,

где 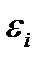— электродвижущая сила индукции; N — число витков кон­тура; Y — потокосцепление.

Частные случаи применения основного закона электромагнитной индукции:

а) разность потенциалов U на концах проводника длиной I, движущегося со скоростью u в однородном магнитном поле,

U=B∙l∙u∙sina,

где a — угол между направлениями векторов скорости u и магнит­ной индукции В;

б) электродвижущая сила индукции 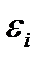, возникающая в рамке, содержащей N витков, площадью S, при вращении рамки с угловой скоростью со в однородном магнитном поле с индукцией В

,

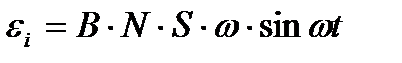где wt — мгновенное значение угла между вектором В и вектором нормали n к плоскости рамки.

• Количество электричества Q, протекающего в контуре,

,

где R — сопротивление контура; DY — изменение потокосцепления.

•Электродвижущая сила самоиндукции возникающая в замкнутом контуре при изменении силы тока в нем,

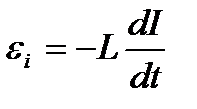, или ,

где L — индуктивность контура.

• Потокосцепление контура Y=L∙I, где L — индуктивность контура.

• Индуктивность соленоида (тороида)

.

Во всех случаях вычисления индуктивности соленоида (тороида) с сердечником по приведенной формуле для определения магнит­ной проницаемости следует пользоваться графиком зависимости В от Н, а затем формулой

.

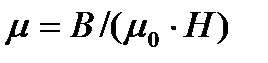• Мгновенное значение силы тока I в цепи, обладающей актив­ным сопротивлением R и индуктивностью L:

а) после замыкания цепи

,

где ε-ЭДС источника тока; t—время, прошедшее после замы­кания цепи;

б) после размыкания цепи

,

где l₀- сила тока в цепи при t=0, t - время, прошедшее с момен­та размыкания цепи.

• Энергия W магнитного поля, создаваемого током в замкнутом контуре индуктивностью L, определяется формулой

,

где I — сила тока в контуре.

• Объемная (пространственная) плотность энергии однородного магнитного поля (например, поля длинного соленоида)

.

• Формула Томсона. Период собственных колебаний в контуре без активного сопротивления

,

где L — индуктивность контура; С — его электроемкость.

• Связь длины электромагнитной волны с периодом Т и час­тотой υ колебаний

или ,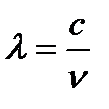

где с — скорость электромагнитных волн в вакууме (с=3∙10⁸м/с).

• Скорость электромагнитных волн в среде

где ε- диэлектрическая проницаемость; μ - магнитная проницае­мость среды.