Вероятность суммы двух несовместных событий равняется сумме вероятностей этих событий.
Запишем теорему сложения символически:
Р(А + В) = Р(А)+Р(В),
где Р — вероятность соответствующего события (событие указывается в скобках).
Пример. У больного наблюдается желудочное кровотечение. Этот симптом регистрируется при язвенной эрозии сосуда (событие А), разрыве варикозно-расширенных вен пищевода (событие В), раке желудка (событие С), полипе желудка (событие D), геморрагическом диатезе (событие F), механической желтухе (событие Е) и конечном гастрите (событие G).
Врач, основываясь на анализе статистических данных, присваивает каждому событию значение вероятности:
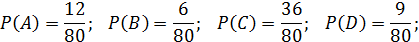
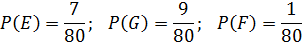
Всего врач имел 80 больных с желудочным кровотечением (n = 80), из них у 12 была язвенная эрозия сосуда ( 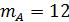 ), у 6 — разрыв варикозно-расширенных вен пищевода (
), у 6 — разрыв варикозно-расширенных вен пищевода ( 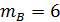 ), у 36 — рак желудка (
), у 36 — рак желудка ( 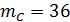 ) и т. д.
) и т. д.
Для назначения обследования врач хочет определить вероятность того, что желудочное кровотечение связано с заболеванием желудка (событие I):
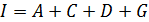
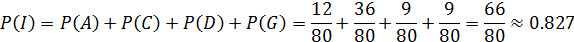
Вероятность того, что желудочное кровотечение связано с заболеванием желудка, достаточно высока, и врач может определить тактику обследования, исходя из предположения о заболевании желудка, обоснованном на количественном уровне с помощью теории вероятностей.