Линейная регрессия
Математическое уравнение, которое оценивает линию простой линейной регрессии:
Y = a + bx
х – называется предиктором – независимой или объясняющей переменной.
Для данной величины х, Y — значение переменной у (называемой зависимой, выходной переменной, или переменной отклика), которое расположено на линии оценки. Это есть значение, которое мы ожидаем для у (в среднем), если мы знаем величину х, и называется она «предсказанное значение у» (рис. 5).
а – свободный член (пересечение) линии оценки; это значение Y, когда х=0.
b – угловой коэффициент или градиент оценённой линии; он представляет собой величину, на которую Y увеличивается в среднем, если мы увеличиваем х на одну единицу (рис. 5). Коэффициент b называют коэффициентом регрессии.
Например: при увеличении температуры тела человека на 1оС, частота пульса увеличивается в среднем на 10 ударов в минуту.

Рисунок 5. Линия линейной регрессии, показывающая коэффициент а и угловой коэффициент b (величину возрастания Y при увеличении х на одну единицу)
Математически решение уравнения линейной регрессии сводится к вычислению параметров а и b таким образом, чтобы точки исходных данных корреляционного поля как можно ближе лежали к прямой регрессии.
Статистическое использование слова «регрессия» исходит из явления, известного как регрессия к среднему, приписываемого Френсису Гальтону (1889). Он показал, что, хотя высокие отцы имеют тенденцию иметь высоких сыновей, средний рост сыновей меньше, чем у их высоких отцов. Средний рост сыновей «регрессировал» или «двигался вспять» к среднему росту всех отцов в популяции. Таким образом, в среднем высокие отцы имеют более низких (но всё-таки высоких) сыновей, а низкие отцы имеют сыновей более высоких (но всё-таки довольно низких).
Мы наблюдаем регрессию к среднему при скрининге и клинических исследованиях, когда подгруппа пациентов может быть выбрана для лечения потому, что их уровни определённой переменной, скажем, холестерина, крайне высоки (или низки). Если это измерение через некоторое время повторяется, средняя величина второго считывания для подгруппы обычно меньше, чем при первом считывании, имея тенденцию (т.е. регрессируя) к среднему, подобранному по возрасту и полу в популяции, независимо от лечения, которое они могут получить. Пациенты, набранные в клиническое исследование на основе высокого уровня холестерина при их первом осмотре, таким образом, вероятно, покажут в среднем падение уровня холестерина при втором осмотре, даже если в этот период они не лечились.
Часто метод регрессионного анализа применяется для разработки нормативных шкал и стандартов физического развития.
Насколько хорошо линия регрессии согласуется с данными, можно судить, рассчитав коэффициент R (обычно выраженный в процентах и называемый коэффициентом детерминации), который равняется квадрату коэффициента корреляции (r2). Он представляет собой долю или процент дисперсии у, который можно объяснить связью с х, т.е. долю вариации признака-результата, сложившуюся под влиянием независимого признака. Может принимать значения в диапазоне от 0 до 1, или соответственно от 0 до 100%. Разность (100% - R) представляет собой процент дисперсии у, который нельзя объяснить этим взаимодействием.
Пример
Соотношение между ростом (измеренным в см) и систолическим артериальным давлением (САД, измеренным в мм рт. ст.) у детей. Мы провели анализ парной линейной регрессии зависимости САД от роста (рис. 6). Имеется существенное линейное соотношение между ростом и САД.
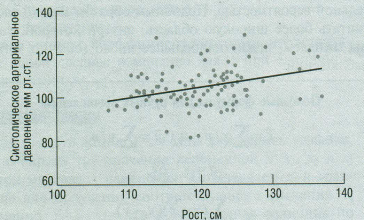
Рисунок 6. Двумерный график, показывающий соотношение между систолическим артериальным давлением и ростом. Изображена оценённая линия регрессии, систолическое артериальное давление.
Уравнение линии оценённой регрессии имеет следующий вид:
САД = 46,28 + 0,48 х рост.
В этом примере свободный член не представляет интереса (рост, равный нулю, явно вне диапазона величин, наблюдаемых в исследовании). Однако мы можем интерпретировать угловой коэффициент; предсказано, что у этих детей САД увеличивается в среднем на 0,48 мм рт.ст. при увеличении роста на один сантиметр
Мы можем применить уравнение регрессии для предсказания САД, которое мы ожидаем у ребёнка при данном росте. Например, ребёнок ростом 115 см имеет предсказанное САД, равное 46,28 + (0,48 х 115)=101,48 мм рт. ст., ребёнок ростом 130 имеет предсказанное САД, 46,28 + (0,48 х 130) = 108,68 мм рт. ст.
При расчете коэффициента корреляции, установлено, что он равен 0,55, что указывает на прямую корреляционную связь средней силы. В этом случае коэффициент детерминации r2 = 0,552 = 0,3. Таким образом, можно сказать, что доля влияния роста на уровень артериального давления у детей не превышает 30%, соответственно на долю других факторов приходится 70% влияния.
Линейная (простая) регрессия ограничивается рассмотрением связи между зависимой переменной и только одной независимой переменной. Если в связи присутствует более одной независимой переменной, тогда нам необходимо обратиться к множественной регрессии. Уравнение для такой регрессии выглядит так:
y = a + bx1+b2x2 +.... + bnхn
Можно интересоваться результатом влияния нескольких независимых переменных х1, х2, .., хn на переменную отклика у. Если мы полагаем, что эти х могут быть взаимозависимы, то не должны смотреть по отдельности на эффект изменения значения одного х на у, но должны одновременно принимать во внимание величины всех других х.
Пример
Поскольку между ростом и массой тела ребёнка существует сильная зависимость, можно поинтересоваться, изменяется ли также соотношение между ростом и систолическим артериальным давлением, если принять во внимание также и массу тела ребёнка и его пол. Множественная линейная регрессия позволяет изучить совместный эффект этих нескольких независимых переменных на у.
Уравнение множественной регрессии в этом случае может иметь такой вид:
САД=79,44 –(0,03 х рост)+ (1,18 х вес) + (4,23 х пол)*
* - (для признака пол используют значения 0 – мальчик, 1 - девочка)
Согласно этому уравнению, девочка, рост которой 115 см и масса тела 37 кг, будет иметь прогнозируемое САД:
САД = 79,44 – (0,03 х 115) + (1,18 х 37) + (4,23 х 1) = 123,88 мм.рт.ст.
Логистическая регрессия очень похожа на линейную; её применяют, когда есть интересующий нас бинарный исход (т.е. наличие/отсутствие симптома или субъекта, который имеет/не имеет заболевания) и ряд предикторов. Из уравнения логистической регрессии можно определить, какие предикторы влияют на исход, и, используя значения предикторов пациента, оценить вероятность того, что он/она будет иметь определённый исход. Например: возникнут или нет осложнения, будет лечение эффективным или не будет.
Начинают создания бинарной переменной, чтобы представить эти два исхода (например, «имеет болезнь»=1, «не имеет болезни»=0). Однако мы не можем применить эти два значения как зависимую переменную в анализе линейной регрессии, поскольку предположение нормальности нарушено, и мы не можем интерпретировать предсказанные величины, которые не равны нулю или единице. Фактически, вместо этого мы берём вероятность того, что субъект классифицируется в ближайшую категорию (т.е. «имеет болезнь») зависимой переменной, и чтобы преодолеть математические трудности, применяют логистическое, преобразование, в уравнении регрессии — натуральный логарифм отношения вероятности «болезни» (p) к вероятности «нет болезни» (1-p).

Интегративный процесс, называемый методом максимального правдоподобия, а не обычная регрессия (так как мы не можем применить процедуру линейной регрессии) создаёт из данных выборки оценку уравнения логистической регрессии
logit (p) = a + bx1+b2x2 +.... + bnхn
• .logit (р) — оценка значения истинной вероятности того, что пациент с индивидуальным набором значений для х1 ... хn имеет заболевание;
• а — оценка константы (свободный член, пересечение);
• b1, b2,... ,bn — оценки коэффициентов логистической регрессии.
1. Вопросы по теме занятия:
1. Дайте определение функциональной и корреляционной связи.
2. Приведите примеры прямой и обратной корреляционной связи.
3. Укажите размеры коэффициентов корреляции при слабой, средней и сильной связи между признаками.
4. В каких случаях применяется ранговый метод вычисления коэффициента корреляции?
5. В каких случаях применяется расчет коэффициента корреляции Пирсона?
6. Каковы основные этапы вычисления коэффициента корреляции ранговым методом?
7. Дайте определение «регрессии». В чем сущность метода регрессии?
8. Охарактеризуйте формулу уравнения простой линейной регрессии.
9. Дайте определение коэффициента регрессии.
10. Какой можно сделать вывод, если коэффициент регрессии веса по росту равен 0,26кг/см?
11. Для чего используется формула уравнения регрессии?
12. Что такое коэффициент детерминации?
13. В каких случаях используется уравнение множественной регрессии.
14. Для чего применяется метод логистической регрессии?