ВЫБОР ТИПА РЕГУЛЯТОРА И ВЫВОД ФОРМУЛ ДЛЯ РАСЧЕТА ПАРАМЕТРОВ ЕГО НАСТРОЙКИ

ИССЛЕДОВАНИЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ СИНТЕЗИРОВАННОЙ МЕТОДОМ СИММЕТРИЧНОГО ОПТИМУМА

Цель работы: Получение практических навыков синтеза системы автоматического регулирования методом симметричного оптимума. Анализ влияния неточности определения параметров модели объекта регулирования на качество переходных процессов в системе.

 

ОСНОВНЫЕ ПОЛОЖЕНИЯ И ОПРЕДЕЛЕНИЯ

 

В состав объекта регулирования могут входить не только инерционные звенья 1-го порядка, пропорциональные звенья, но и звенья интегрирующего характера. В последнем случае компенсация наибольшей инерционности или двух самых больших инерционностей 1-го порядка уже не может дать необходимого результата, так как интегральному звену объекта противопоставляется интегральный характер регулятора. Это приводит к синусоидальным колебаниям регулируемой величины [1,с.143-149].

В связи с этим, синтез системы с объектом, содержащим интегрирующее звено, необходимо осуществлять не методом модального оптимума, а методом симметричного оптимума.

В основе метода симметричного оптимума положен тот же критерий оптимальности, что и в методе модального оптимума, а именно критерий оптимального модуля [см. лабораторную работу N 6]. Однако значение постоянной времени интегрирования Ти определяется, исходя из нового условия оптимизации.

 

ВЫБОР ТИПА РЕГУЛЯТОРА И ВЫВОД ФОРМУЛ ДЛЯ РАСЧЕТА ПАРАМЕТРОВ ЕГО НАСТРОЙКИ

 

1.1.1. Объект регулирования включает одно интегрирующее звено и "n" инерционных звеньев 1-го порядка с малыми постоянными времени.

 

Передаточная функция объекта регулирования имеет следующий вид:

где 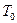- постоянная интегрирования; .

В этом случае целесообразно применить ПИ-регулятор.

Передаточная функция разомкнутой системы имеет вид:

(1)

Тогда основная передаточная функция замкнутой системы примет следующий вид:

(2)

Для обеспечения близости амплитудно-частотной характеристики (АЧХ) к единице необходимо потребовать выполнения следующих условий оптимизации (см. формулы (5) лабораторной работы N 6):

 

(3)

С учетом того, что , , и получим:

(4)

Подставив выражение (4) в (2) для Ф(р), получим стандартную передаточную функцию для симметричного оптимума :

(5)

Из выражения (4) следует, что переходной процесс в системе, синтезированной методом симметричного оптимума, зависит только от суммы постоянных времени звеньев 1-го порядка.

Стандартный переходной процесс в АСР синтезированной методом симметричного оптимума, соответствующий стандартной передаточной функции (5) имеет следующие прямые показатели качества:

- время нарастания tн=3,1 ;

- время регулирования tр=16,5 ;

- перерегулирование DY=43,4%.

 

1.1.2. Объект регулирования включает интегрирующее звено и "n" инерционных звеньев 1-го порядка с одной большой постоянной времени.

 

Передаточная функция объекта регулирования задана следующей передаточной функцией:

где Т1 - большая постоянная времени.

В этом случае имеет смысл для повышения быстродействия системы принять меры для компенсации инерционности Т1.

Необходимость компенсации большей инерционности и наличие интегрирующего звена в составе объекта требует применения ПИД-регулятора.

Тогда из уравнения разомкнутой системы:

(6)

с учетом условия компенсации:

Tд=T1 (7)

получим передаточную функцию, определяемую выражением (1) (см. п.1.1.1.). Формула (4) расчета параметров Ти и Кp становятся справедливыми и для ПИД-регулятора. Поэтому основная передаточная функция системы и в этом случае соответствует стандартному выражению (5)

 

1.1.3. Объект регулирования включает только "n" инерционных звеньев 1-го порядка.

 

Если в составе объекта имеется инерционное звено 1-го порядка с постоянной времени , то это звено в первом приближении можно рассматривать как интегрирующее звено.

При таком представлении ПИ-регулятор можно настраивать методом симметричного оптимума с использованием формул (4):

(8)

В этом случае время нарастания будет несколько большим, а перерегулирование - меньшим, чем в стандартном варианте (см. п.1.1.1.), когда объект содержит интегрирующее звено.

Замечание: При Т1=4 переходной процесс в системе регулирования соответствует стандартному для метода модального оптимума.