Теоретическое обоснование работы

При отводе маятника на угол φ₀ (рис. 7.1) от положения ус­тойчивого равновесия совершаются колебательные движения. Рассмотрим маятник в произвольном положении, определяемом утлом φ. Проводим оси координат ОХУ так, чтобы ось ОХ была перпендикулярна оси маятника, а ось ОУ направлена вдоль линии ОВ (рис. 7.1).

Изобразим действующую на маятник силу тяжести Р, реакции опор Х₀ и У₀ (силой тяжести стержня маятника пренебрегаем).

 

 

 

Рис 7.1. Схема к исследованию динамических реакций опоры.

Присоединим к ним силы инерции маятника, приведя их к центру О . Силы инерции представлены двумя составляющими

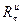и , а. также парой с моментом М₀. Модули их имеют зна­чения:

(7.1)

(7.2)

(7.3)

где l - длина стержня маятника (l = ОВ);

ω, ε - угловая скорость и угловое ускорение маятника.
Составляя для этой плоской системы сил уравнения равновесия и получим:
x₀-psinφ + 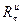= 0, (7.4)

y₀-pcosφ-R =0, (7.5)

(7.6)

Отсюда реакции опоры

x₀-psinφ -R =0, (7.7)

y₀-pcosφ+ R^u_n=0. (7.8)

В выражениях (7.7) и (7.8) составляющие р sinφи pcosφ

являются проекциями статической реакции, а 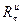и - проекциями динамической реакции. Как видно из выражений (7.1) и(7.2) проекции динамической реакции зависят от угловой скоро­сти ω, углового ускорения е маятника.

Для определения угловой скорости маятника в произвольном положении воспользуемся теоремой об изменении кинетической энергии. Учитывая, что при ω = ω₀ кинетическая энергия маятника Т₀ = 0, получим:

Откуда, приняв J₀=pl² /g, находим:

ω² = 2g(cos φ - cos φ₀)/l . Угловое ускорение s получим из выражения (7.6), предварительно заменив его выражением (7.3), т. е. по формуле:

е = gsinφ/l

При найденных значениях ε и ω² равенства (7.1) и (7.2) при­мут вид:

R = р sinφ,

R^u_n = 2_p(cosφ- cosφ₀)

Тогда модуль динамической реакции определяется по Формуле:

(7.9)

Как видно из выражения (7.9), динамическая реакция является величиной переменной. В момент, когда маятник проходит положение устойчивого равновесия (φ = 0) динамическая реакция примет максимальное значение, т. е. выражение (7.9) пред­ставится в виде:

R_g = 2р (1- cos φ₀)