Теоретическое обоснование работы

Исследуем движение диска, подвешенного на жестком моно­филярном подвесе с возможностью совершать крутильные коле­бания.

Повернув диск на некоторый, угол φ (рис. 5.1) вокруг верти­кальной оси OZ, сообщим ему крутильные колебания.

Рис 5.1. Схема к исследованию крутильных колебаний диска.

Дифференциальное уравнение движения диска при этом имеет вид:

J$ = -Mz, (5.1)

где М2 - вращающий момент сил упругости жесткого монофиляр­ного подвеса.

Вращающий момент сил упругости жесткого монофилярного подвеса

Mz = сφ

где С - крутильная жесткость монофилярного подвеса, Н∙м/рад.

 

 

Тогда выражение (5.1) примет вид:

Jg = cφ, (5.2)

Разделив обе части равенства на Jg и обозначив С /Jg = К2 , после преобразований получим дифференциальное уравнение крутильных колебаний диска в воде:

φ = с1 sin kt + c2 cos kt;

где Сj, C2 - постоянные интегрирования.

Полагая, что в начальный момент t = 0, диск повернут на ма­лый угол φ = φ0 иотпущен без начальной скорости (φ0 = 0), найдем для постоянных интегрирования С} = О, С2 = φо • Тогда закон малых колебаний диска при данных начальных условиях: будет иметь окончательный вид:

φ = φ0 cos kt (5.3)

Следовательно, малые крутильные колебания диска являются гармоническими. При этом период колебаний определяется фор­мулой:

Tg=2π (5.4)

Как видно из этой формулы, период крутильных колебаний зависит только от момента инерции механической системы и кру­тильной жесткости подвеса. Тогда, если предполагать, что систе­ма состоит из диска и дополнительного тела (исследуемого или эталонного), можно считать действительными следующие выра­жения:

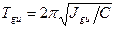(5.5)

(5.6)

где Tgu, Tg3 - периоды колебаний соответственно диска с иссле­дуемым телом и диска с эталонным телом;

Jg, Jэ, Jgll, Jg3 - моменты инерции соответственно диска, эта­лонного тела, диска с исследуемым телом и диска с эталонным телом.

Решая систему уравнений (5.4) и (5.6), получим:

(5.7)

 

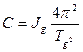(5.8)

Находим момент инерции диска с исследуемым телом Jgu из уравнения (5.5):

(5.9)

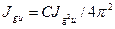
С другой стороны:

Jgu=Jg+Ju (5.10)

где Ju - момент инерции исследуемого тела. Из выражений (5.9) и (5.10) находим:

Или с учетом выражений (5.7) и (5.8) после преобразований получим:

(5.11)

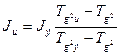
Таким образом, определив периоды крутильных колебаний диска, диска с эталонным телом и диска с исследуемым телом, можно рассчитать по формуле (5.11) момент инерции последнего.