Теоретическое обоснование работы

Процесс преобразования электрической энергии в механиче­скую сопровождается потерями. В них существенную долю со­ставляет механическая часть потерь.

Исследуем механические потери в асинхронном электродви­гателе с короткозамкнутым ротором, расположенным горизон­тально.

Ниже приведены технические данные электродвигателя, не­обходимые для исследований.

Технические данные лабораторной установки

1. Тип электродвигателя - асинхронный с короткозамкнутым
ротором.

2. Момент инерции ротора J_x . кг-м²
0,0017

3. Угловая скорость вращения ротора ω₀ , рад/с
104,5

При подключении электродвигателя к сети питания возникает движущий момент в роторе. В результате ротор начинает вра­щаться. Через некоторое время угловая скорость стабилизируется, становится равной с со₀.

При отключении электродвигателя от сети питания ротор продолжает вращаться по инерции. Однако из-за механических потерь угловая скорость вращения ротора постепенно падает, и через определенное время он останавливается. При этом механи­ческие потери складываются из момента трения в опорах и мо­мента сил сопротивления воздуха при вращении ротора (рис. 3.1).

Рис 3.1. Схема к исследованию механических потерь в электродви­гателе .

Момент трения в опорах ротора является постоянной величи­ной, зависящей от сил реакции и коэффициента трения в опорах, т. е. определяется по формуле:

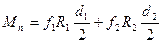
Гдеf₁, f₂ - условные коэффициенты трения в подшипниках;

R₁, R₂ - реакции опор;

d_b d₂ - диаметры цапф ротора под подшипники (часто при­нимают оба подшипника одинаковыми).

Момент сил сопротивления воздуха пропорционален угловой скорости вращения ротора, т. е. определяется по формуле:

М_в =μω

где μ. - коэффициент сопротивления воздуха при вращении ро­тора;

ω - угловая скорость вращения ротора.

Момент сил сопротивления воздуха определяется теоретиче­ски с невысокой точностью, так как большие трудности возника­ют в определении коэффициента сопротивления воздуха μ. По­этому для практической оценки механических потерь в электро­двигателе ограничимся определением среднего значения момента М_Ср сил сопротивления вращению ротора электродвигателя.

Рассмотрим вращательное движение ротора после отключения от сети питания электродвигателя. При этом движение ротора можно описать дифференциальным уравнением вида:

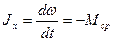(3.1)

 

где J_x - момент инерции ротора;

со - текущее значение угловой скорости ротора. Разделяя пе­ременные, взяв от обеих частей равенства соответствующие ин­тегралы, получим:

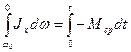
где ω₀ - угловая скорость вращения ротора в момент отключения электродвигателя от сети питания;

t - время свободного вращения ротора до полной остановки. Откуда после преобразований

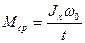(3.2)