КОНТРОЛЬНАЯ РАБОТА
ТЕОРИЯ ВЕРОЯТНОСТЕЙ
Теория вероятностей. Определение вероятности. Классическое и статистическое определение вероятности. Геометрические вероятности. Основные теоремы. Теорема сложения и умножения вероятностей. Вероятность появления хотя бы одного события. Формула полной вероятности. Формула Бейеса. Повторение испытаний. Формула Бернулли. Локальная и интегральная теоремы Лапласа. Отклонение относительной частоты от постоянной вероятности в независимых испытаниях. Наивероятнейшее число появлений события в независимых испытаниях. Дискретные случайные величины (д.с.в.). Закон распределения вероятностей д.с.в.. Законы биномиальные и Пуассона. Простейший поток событий. Числовые характеристики д.с.в.. Теоретические моменты. Закон больших чисел. Неравенство Чебышева. Теорема Чебышева. Функции и плотности распределения вероятностей случайных величин. Функции распределения вероятностей с.в.. Плотность распределения вероятностей непрерывной с.в. (н.с.в.) Числовые характеристики н.с.в. Равномерное, нормальное и показательное распределения. Функция надежности. Распределение функции одного и двух случайных аргументов. Функция одного случайного аргумента. Функция двух случайных аргументов.
КОНТРОЛЬНАЯ РАБОТА
Задание 1.В партии из N деталей имеется n стандартных. Наудачу отобраны m деталей. Найти вероятность того, что среди отобранных деталей ровно k стандартных.
| N = 10, n =4, m =7, k = 3 | N = 15, n =10, m =5, k = 3 | N =12, n =8, m = 9, k = 5 | |||
| N = 6, n =4, m =3, k = 2 | N =14, n = 9, m = 6, k = 4 | N =8, n =5, m = 6, k = 4 | |||
| N =18, n =14, m =9, k = 7 | N =20, n =14, m =15,k =12 | N =17, n =12, m =9, k= 7 | |||
| N=22, n=18, m =20, k=17 | N =12, n =8, m = 9, k = 5 | N = 15, n =10, m =5, k = 3 | |||
| N = 10, n =4, m =7, k = 3 | N=22, n=18, m =20, k=17 | N =14, n = 9, m = 6, k = 4 | |||
| N = 6, n =4, m =3, k = 2 | N = 15, n =10, m =5, k = 3 | N =8, n =5, m = 6, k = 4 | |||
| N =18, n =14, m =9, k = 7 | N =14, n = 9, m = 6, k = 4 | N =17, n =12, m =9, k= 7 | |||
| N =20, n =14, m =15,k =12 | N =17, n =12, m =9, k= 7 | N =12, n =8, m = 9, k = 5 | |||
| N=22, n=18, m =20, k=17 | N = 10, n =4, m =7, k = 3 | N =8, n =5, m = 6, k = 4 | |||
| N =20, n =14, m =15,k =12 | N = 6, n =4, m =3, k = 2 | N =18, n =14, m =9, k = 7 |
Задание 2.Батарея из трех орудий произвела залп, причем два снаряда попали в цель. Найти вероятность того, что первое орудие дало попадание, если вероятности попадания в цель первым, вторым и третьим орудиями соответственно равны 
, 
, 
.
1.  ,  , 
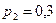| 2. , ,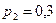
| 3. ,  , 
|
4. ,  , 
| 5.  , ,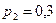
| 6. ,  ,
|
7.  , ,
| 8.  , ,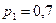
| 9.  ,  ,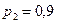
|
10. ,  , 
| 11. , ,
| 12. , ,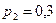
|
| 13. , ,
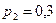| 14. , ,
| 15. , ,
|
| 16. , ,
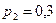| 17. , ,
| 18. , ,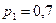
|
| 19. , ,
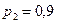| 20. , ,
| 21. , ,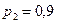
|
| 22. , ,
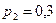| 23. , ,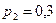
| 24. , ,
|
| 25. , ,
| 26. , ,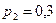
| 27. , ,
|
| 28. , ,
| 29. , ,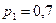
| 30. , ,
|
Задание 3.В семье n детей. Найти вероятность того, что среди этих детей: а) k мальчиков; б) не более k мальчиков; в) более k мальчиков; Вероятность рождения мальчика принять равной 0,51.
| n = 5, k = 2, m = 3 | n = 7, k = 4, m = 3 | n = 6, k = 2, m = 4 | |||
| n = 8, k = 6, m = 2 | n = 5, k = 3, m = 2 | n = 7, k = 5, m = 2 | |||
| n = 4, k = 3, m = 1 | n = 6, k = 5, m = 1 | n = 5, k = 4, m = 1 | |||
| n = 6, k = 4, m = 2 | n = 6, k = 2, m = 4 | n = 7, k = 4, m = 3 | |||
| n = 5, k = 2, m = 3 | n = 8, k = 6, m = 2 | n = 6, k = 4, m = 2 | |||
| n = 7, k = 5, m = 2 | n = 4, k = 3, m = 1 | n = 5, k = 3, m = 2 | |||
| n = 6, k = 5, m = 1 | n = 5, k = 4, m = 1 | n = 6, k = 2, m = 4 | |||
| n = 4, k = 3, m = 1 | n = 7, k = 5, m = 2 | n = 6, k = 5, m = 1 | |||
| n = 6, k = 4, m = 2 | n = 7, k = 4, m = 3 | n = 5, k = 2, m = 3 | |||
| n = 8, k = 6, m = 2 | n = 5, k = 3, m = 2 | n = 5, k = 4, m = 1 |
Задание 4.Вероятность появления события в каждом из N независимых испытаний постоянна и равна р. Найти вероятность того, что событие появится: а) ровно k раз;
б) не менее k раз и не более k1 раз; в) не менее k раз; г) не более (k – 1) раз.
1.N = 100, p = 0,8, k = 75,
 =90
| 2.N = 100, p = 0,8, k = 85,
=95
|
| 3.N = 100, p = 0,8, k = 65,
=75
| 4.N = 100, p = 0,9, k = 76,
=92
|
| 5.N = 120, p = 0,8, k = 90,
=100
| 6.N = 120, p = 0,8, k = 100,
=110
|
| 7.N = 100, p = 0,9, k = 85,
=90
| 8.N = 100, p = 0,8, k = 80,
=90
|
| 9.N = 110, p = 0,8, k = 90,
=100
| 10.N = 130, p = 0,9, k = 110, =120
|
| 11.N = 120, p = 0,8, k = 100, =110
| 12.N = 120, p = 0,8, k = 90, =100
|
| 13.N = 100, p = 0,8, k = 80, =90
| 14.N = 100, p = 0,9, k = 85, =90
|
| 15.N = 100, p = 0,8, k = 75, =90
| 16.N = 100, p = 0,8, k = 85, =95
|
| 17.N = 100, p = 0,8, k = 65, =75
| 18.N = 100, p = 0,9, k = 76, =92
|
| 19.N = 110, p = 0,8, k = 90, =100
| 20.N = 130, p = 0,9, k = 110, =120
|
| 21.N = 120, p = 0,8, k = 90, =100
| 22.N = 120, p = 0,8, k = 100, =110
|
| 23.N = 100, p = 0,9, k = 85, =90
| 24.N = 100, p = 0,8, k = 80, =90
|
| 25.N = 100, p = 0,8, k = 75, =90
| 26.N = 100, p = 0,8, k = 85, =95
|
| 27.N = 100, p = 0,8, k = 65, =75
| 28.N = 100, p = 0,9, k = 76, =92
|
| 29.N = 130, p = 0,9, k = 110, =120
| 30.N = 110, p = 0,8, k = 90, =100
|
Задание 5.Вероятность положительного исхода опыта, который проводит химик , в каждом опыте одинакова и равна р. Выписать ряд распределения числа неудачных опытов из n проведенных. Найти: 1) математическое ожидание; 2) дисперсию; 3) среднее квадратическое отклонение; 4) построить график ряда распределения дискретной случайной величины.
| 1.р = 0,7, n = 4 | 2.р = 0,9 , n = 4 | 3.р = 0,85, n = 4 | 4.р = 0,7 , n = 4 | 5.р = 0,9 , n = 5 |
| 6.р = 0,75, n = 3 | 7.р = 0,8 , n = 4 | 8.р = 0,8 , n = 5 | 9.р = 0,85, n = 4 | 10.р = 0,6, n = 4 |
| 7.р = 0,8 , n = 4 | 8.р = 0,8 , n = 5 | 1.р = 0,7, n = 4 | 2.р = 0,9 , n = 4 | 3.р = 0,85, n = 4 |
| 4.р = 0,7 , n = 4 | 6.р = 0,75, n = 3 | 5.р = 0,9 , n = 5 | 10.р = 0,6, n = 4 | 5.р = 0,9 , n = 5 |
| 6.р = 0,75, n = 3 | 10.р = 0,6, n = 4 | 9.р = 0,85, n = 4 | 1.р = 0,7, n = 4 | 2.р = 0,9 , n = 4 |
| 3.р = 0,85, n = 4 | 4.р = 0,7 , n = 4 | 8.р = 0,8 , n = 5 | 7.р = 0,8 , n = 4 | 9.р = 0,85, n = 4 |
Задание 6.Непрерывная случайная величина Х задана интегральной функцией распределения F(x). Найти: а) вероятность попадания случайной величины Х в интервал (а; b);
б) плотность распределения вероятностей случайной величины Х (дифференциальную функцию распределения); в) математическое ожидание М(Х); г) дисперсию D(X);
д) среднее квадратическое отклонение 
.
1.
а = -2; b = -1
| 2.
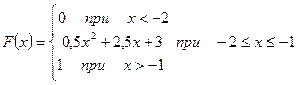а = -2; b = -1,5
|
3.
а = 3,5; b = 4
| 4.
а = -0,5; b = 0,5
|
5.
а = 3; b = 3,5
| 6.
а = 3,5; b = 4
|
7.
а = -0,5; b = 1
| 8.
а = -2; b = -1,5
|
9.
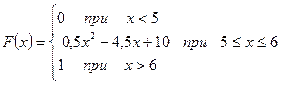а = 5; b = 5,5
| 10.
а = 2; b = 3
|
| 11.
а = 2; b = 3
| 12.
а = -2; b = -1
|
| 13.
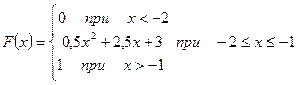а = -2; b = -1,5
| 14.
а = -2; b = -1,5
|
| 15.
а = 2; b = 3
| 16.
а = -0,5; b = 0,5
|
| 17.
а = 3,5; b = 4
| 18.
а = 3,5; b = 4
|
| 19.
а = 3; b = 3,5
| 20.
а = -0,5; b = 1
|
| 21.
а = -2; b = -1
| 22.
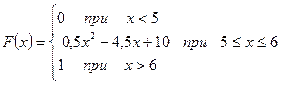а = 5; b = 5,5
|
| 23.
а = -0,5; b = 0,5
| 24.
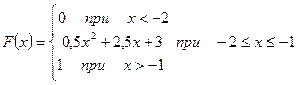а = -2; b = -1,5
|
| 25.
а = 3,5; b = 4
| 26.
а = 3,5; b = 4
|
| 27.
а = -0,5; b = 1
| 28.
а = 3; b = 3,5
|
| 29.
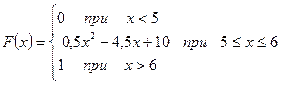а = 5; b = 5,5
| 30.
а = -2; b = -1,5
|