Про обозначения
Базовый уровень, время – 3 мин)
Тема: Построение и анализ таблиц истинности логических выражений.
Про обозначения
К сожалению, обозначения логических операций И, ИЛИ и НЕ, принятые в «серьезной» математической логике (Ù,Ú,), неудобны, интуитивно непонятны и никак не проявляют аналогии с обычной алгеброй. Автор, к своему стыду, до сих пор иногда путает Ù и Ú. Поэтому на его уроках операция «НЕ» обозначается чертой сверху, «И» – знаком умножения (поскольку это все же логическое умножение), а «ИЛИ» – знаком «+» (логическое сложение).
В разных учебниках используют разные обозначения. К счастью, в начале задания ЕГЭ приводится расшифровка закорючек (Ù,Ú,), что еще раз подчеркивает проблему.
Что нужно знать:
· условные обозначения логических операций
A, 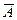 не A (отрицание, инверсия)
не A (отрицание, инверсия)
A Ù B,  A и B (логическое умножение, конъюнкция)
A и B (логическое умножение, конъюнкция)
A Ú B, 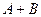 A или B (логическое сложение, дизъюнкция)
A или B (логическое сложение, дизъюнкция)
A→B импликация (следование)
AºB эквивалентность (равносильность)
· операцию «импликация» можно выразить через «ИЛИ» и «НЕ»:
A→B = A Ú Bили в других обозначениях A→B = 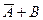
· иногда для упрощения выражений полезны формулы де Моргана:
(A Ù B) = A Ú B 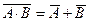
(A Ú B) = A Ù B 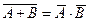
· если в выражении нет скобок, сначала выполняются все операции «НЕ», затем – «И», затем – «ИЛИ», «импликация», и самая последняя – «эквивалентность»
· таблица истинности выражения определяет его значения при всех возможных комбинациях исходных данных
· если известна только часть таблицы истинности, соответствующее логическое выражение однозначно определить нельзя, поскольку частичной таблице могут соответствовать несколько разных логических выражений (не совпадающих для других вариантов входных данных);
· количество разных логических выражений, удовлетворяющих неполной таблице истинности, равно 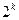 , где
, где 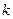 – число отсутствующих строк; например, полная таблица истинности выражения с тремя переменными содержит 23=8 строчек, если заданы только 6 из них, то можно найти 28-6=22=4 разных логических выражения, удовлетворяющие этим 6 строчкам (но отличающиеся в двух оставшихся)
– число отсутствующих строк; например, полная таблица истинности выражения с тремя переменными содержит 23=8 строчек, если заданы только 6 из них, то можно найти 28-6=22=4 разных логических выражения, удовлетворяющие этим 6 строчкам (но отличающиеся в двух оставшихся)
· логическая сумма A + B + C + … равна 0 (выражение ложно) тогда и только тогда, когда все слагаемые одновременно равны нулю, а в остальных случаях равна 1 (выражение истинно)
· логическое произведение A · B · C · … равно 1 (выражение истинно) тогда и только тогда, когда все сомножители одновременно равны единице, а в остальных случаях равно 0 (выражение ложно)
· логическое следование (импликация) А→В равна 0 тогда и только тогда, когда из A (посылка) истинна, а B (следствие) ложно
· эквивалентность АºB равна 1 тогда и только тогда, когда оба значения одновременно равны 0 или одновременно равны 1
Пример задания:
Каждое логическое выражение A и B зависит от одного и того же набора из 5 переменных. В таблицах истинности каждого из этих выражений в столбце значений стоит ровно по 4 единицы. Каково минимально возможное число единиц в столбце значений таблицы истинности выражения A Ú ØB?
Решение:
1) полная таблица истинности каждого выражения с пятью переменными содержит 25 = 32 строки
2) в каждой таблице по 4 единицы и по 28 (= 32 – 4) нуля
3) выражение A Ú ØB равно единице, если A = 1 или B = 0 (или и то, и другое вместе)
4) минимальное количество единиц в таблице истинности выражения A Ú ØB будет тогда, когда в там будет наибольшее число нулей, то есть в наибольшем количество строк одновременно A = 0 и B = 1
5) по условию A = 0 в 28 строках, и B = 1 в 4 строках, поэтому выражение A Ú ØB может быть равно нуля не более чем в 4 строках, оставшиеся 32 – 4 = 28 могут быть равны 1
6) Ответ: 28.
Ещё пример задания:
Дан фрагмент таблицы истинности для выражения F:
| x1 | x2 | x3 | x4 | x5 | F |
Укажите максимально возможное число различных строк полной таблицы истинности этого выражения, в которых значение x1 не совпадает с F.
Решение:
1) полная таблица истинности выражения с пятью переменными содержит 25 = 32 строки
2) в приведённой части таблицы в двух строках значение x1 совпадает с F, а в одной – совпадает
3) во всех оставшихся (неизвестных) 32 – 3 = 29 строках значения x1 и F могут не совпадать
4) всего несовпадающих строк может быть 1 + 29 = 30.
5) Ответ: 30.
Ещё пример задания:
Александра заполняла таблицу истинности для выражения F. Она успела заполнить лишь небольшой фрагмент таблицы:
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | F |
Каким выражением может быть F?
1) x1 Ù x2 Ù x3 Ù x4 Ù x5 Ù x6 Ù x7 Ù x8
2) x1 Ú x2 Ú x3 Ú x4 Ú x5 Ú x6 Ú x7 Ú x8
3) x1 Ù x2 Ù x3 Ù x4 Ù x5 Ù x6 Ù x7 Ù x8
4) x1 Ú x2 Ú x3 Ú x4 Ú x5 Ú x6 Ú x7 Ú x8
Решение:
1) перепишем выражения в более простой форме, заменив «И» (Ù) на умножение и «ИЛИ» (Ú) на сложение:
1) 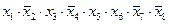
2) 
3) 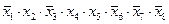
4) 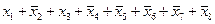
2) в последнем столбце таблицы истинности видим две единицы, откуда сразу следует, что это не может быть цепочка операций «И» (конъюнкций), которая даёт только одну единицу; поэтому ответы 1 и 3 заведомо неверные
3) анализируем первую строку таблицы истинности; мы знаем в ней только два значения -  и
и 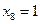
4) для того, чтобы в результате в первой строке получить 0, необходимо, чтобы переменная 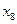 входила в сумму с инверсией (тогда из 1 получится 0!), это условие выполняется для обоих оставшихся вариантов, 2 и 4
входила в сумму с инверсией (тогда из 1 получится 0!), это условие выполняется для обоих оставшихся вариантов, 2 и 4
5) кроме того, переменная 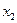 должна входить в выражение без инверсии (иначе соответствующее слагаемое в первой строке равно 1, и это даст в результате 1); этому условию не удовлетворяет выражение 4; остается один возможный вариант – выражение 2
должна входить в выражение без инверсии (иначе соответствующее слагаемое в первой строке равно 1, и это даст в результате 1); этому условию не удовлетворяет выражение 4; остается один возможный вариант – выражение 2
6) Ответ: 2.
Ещё пример задания:
Александра заполняла таблицу истинности для выражения F. Она успела заполнить лишь небольшой фрагмент таблицы:
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | F |
Каким выражением может быть F?
1) x1 Ù x2 Ù x3 Ù x4 Ù x5 Ù x6 Ù x7 Ù x8
2) x1 Ú x2 Ú x3 Ú x4 Ú x5 Ú x6 Ú x7 Ú x8
3) x1 Ù x2 Ù x3 Ù x4 Ù x5 Ù x6 Ù x7 Ù x8
4) x1 Ú x2 Ú x3 Ú x4 Ú x5 Ú x6 Ú x7 Ú x8
1) перепишем выражения в более простой форме, заменив «И» (Ù) на умножение и «ИЛИ» (Ú) на сложение:
1) 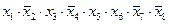
2) 
3) 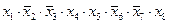
4) 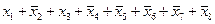
2) в последнем столбце в таблице видим одну единицу и два нуля, поэтому это не может быть дизъюнкция, которая даёт ноль только при одном наборе значений переменных; таким образом, варианты 2 и 4 заведомо неверные, нужно сделать выбор между ответами 1 и 3
3) рассматриваем «особую» строчку таблице, в которой функция равна 1;
4) поскольку мы говорим о конъюнкции, переменная 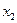 должна входить в неё с инверсией (это выполняется для обоих оставшихся вариантов), а переменная
должна входить в неё с инверсией (это выполняется для обоих оставшихся вариантов), а переменная 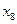 – без инверсии; последнее из этих двух условий верно только для варианта 3, это и есть правильный ответ.
– без инверсии; последнее из этих двух условий верно только для варианта 3, это и есть правильный ответ.
5) Ответ: 3.
Ещё пример задания:
Александра заполняла таблицу истинности для выражения F. Она успела заполнить лишь небольшой фрагмент таблицы:
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | F |
Каким выражением может быть F?
1) x1 Ù x2 Ú x2 Ù x3 Ù x4 Ú x2 Ù x5 Ú x5 Ù x6 Ù x7 Ù x8
2) (x1 Ù x2 Ú x3 Ú x4) Ù (x5 Ú x6 Ú x7 Ú x8)
3) x1 Ù x8 Ú x3 Ù x4 Ù x5 Ú x6 Ù x7 Ù x8
4) x1 Ù x4 Ú x2 Ù x3 Ù x4 Ú x5 Ú x6 Ú x7 Ú x8
Решение:
1) перепишем выражения в более простой форме, заменив «И» (Ù) на умножение и «ИЛИ» (Ú) на сложение:
1) 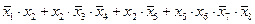
2) 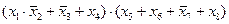
3) 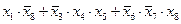
4) 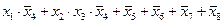
2) cреди заданных вариантов ответа нет «чистых» конъюнкций и дизъюнкций, поэтому мы должны проверить возможные значения всех выражений для каждой строки таблицы
3) подставим в эти выражения известные значения переменных из первой строчке таблицы,  и
и 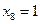 :
:
1) 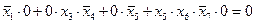
2) 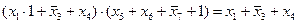
3) 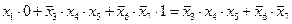
4) 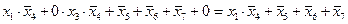
4) видим, что первое выражение при  и
и 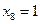 всегда равно нулю, поэтому вариант 1 не подходит; остальные выражения вычислимы, то есть, могут быть равны как 0, так и 1
всегда равно нулю, поэтому вариант 1 не подходит; остальные выражения вычислимы, то есть, могут быть равны как 0, так и 1
5) подставляем в оставшиеся три выражения известные данные из второй строчки таблицы, 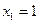 и
и 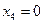 :
:
2) 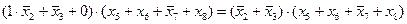
3) 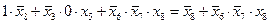
4) 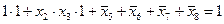
6) видим, что выражение 4 при этих данных всегда равно 1, поэтому получить F=0, как задано в таблице, невозможно; этот вариант не подходит
7) остаются выражения 2 и 3; подставляем в них известные данные из третьей строчки таблицы, 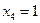 и
и 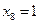 :
:
2) 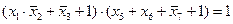
3) 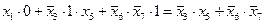
8) Выражение 2 в этом случае всегда равно 1, поэтому оно не подходит (по таблице истинности оно должно быть равно 0); выражение 3 вычислимо, это и есть правильный ответ
9) Ответ: 3.
Ещё пример задания:
Дан фрагмент таблицы истинности выражения F.
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | F |
Какое выражение соответствует F?
1) (x2 ® x1) Ù x3 Ù x4 Ù x5 Ù x6 Ù x7 Ù x8
2) (x2 ® x1) Ú x3 Ú x4 Ú x5 Ú x6 Ú x7 Ú x8
3) (x2 ® x1) Ù x3 Ù x4 Ù x5 Ù x6 Ù x7 Ù x8
4) (x2 ® x1) Ú x3 Ú x4 Ú x5 Ú x6 Ú x7 Ú x8
Решение:
1) перепишем выражение в более простой форме, заменив «И» (Ù) на умножение и «ИЛИ» (Ú) на сложение:

2) в этом задании среди значений функции только одна единица, как у операции «И», это намекает на то, что нужно искать правильный ответ среди вариантов, содержащих «И», «НЕ» и импликацию (это варианты 1 и 3)
3) действительно, вариант 2 исключён, потому что при x4=1 во второй строке получаем 1, а не 0
4) аналогично, вариант 4 исключён, потому что при x5=1 в первой строке получаем 1, а не 0
5) итак, остаются варианты 1 и 3; вариант 1 не подходит, потому что при x6=0 в третьей строке получаем 0, а не 1
6) проверяем подробно вариант 3, он подходит во всех строчках
7) Ответ: 3.
Ещё пример задания:
Дан фрагмент таблицы истинности выражения F.
| x1 | x2 | x3 | x4 | x5 | x6 | F |
Какое выражение соответствует F?
1) (x1 Ù x2) Ú (x3 Ù x4) Ú (x5 Ù x6)
2) (x1 Ù x3) Ú (x3 Ù x5) Ú (x5 Ù x1)
3) (x2 Ù x4) Ú (x4 Ù x6) Ú (x6 Ù x2)
4) (x1 Ù x4) Ú (x2 Ù x5) Ú (x3 Ù x6)
Решение:
1)во-первых, обратим внимание, что в столбце F – все нули, то есть, при всех рассмотренных наборах x1, …, x6 функция ложна
2)перепишем предложенные варианты в более простых обозначениях:
x1×x2 + x3×x4 + x5×x6
x1×x3 + x3×x5 + x5×x1
x2×x4 + x4×x5 + x6×x2
x1×x4 + x2×x5 + x3×x6
3) это суммы произведений, поэтому для того, чтобы функция была равна 0, необходимо, чтобы все произведения были равны 0
4) по таблице смотрим, какие произведения равны 1:
1-я строка: x2×x5, x2×x6 и x5×x6
2-я строка: x3×x6
3-я строка: x2×x4, x2×x6 и x4×x6
5) таким образом, нужно выбрать функцию, где эти произведения не встречаются; отметим их:
x1×x2 + x3×x4 + x5×x6
x1×x3 + x3×x5 + x5×x1
x2×x4 + x4×x5 + x6×x2
x1×x4 + x2×x5 + x3×x6
6) единственная функция, где нет ни одного «запрещённого» произведения – это функция 2
7)Ответ: 2.
Пример задания:
(http://ege.yandex.ru) Дан фрагмент таблицы истинности выражения F.
| x1 | x2 | x3 | x4 | x5 | F |
Одно из приведенных ниже выражений истинно при любых значениях переменных x1, x2,x3, x4, x5. Укажите это выражение.
1) F(x1,x2,x3,x4,x5)®x1
2) F(x1,x2,x3,x4,x5)®x2
3) F(x1,x2,x3,x4,x5)®x3
4) F(x1,x2,x3,x4,x5)®x4
Решение:
1) во всех заданных вариантах ответа записана импликация, она ложна только тогда, когда левая часть (значение функции F) истинна, а правая – ложна.
2) выражение 1 ложно для набора переменных в третьей строке таблицы истинности, где F(…) = 1 и 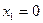 , оно не подходит
, оно не подходит
3) выражение 2 ложно для набора переменных в третьей строке таблицы истинности, где F(…) = 1 и  , оно не подходит
, оно не подходит
4) выражение 3 истинно для всех наборов переменных, заданных в таблице истинности
5) выражение 4 ложно для набора переменных в первой строке таблицы истинности, где F(…) = 1 и 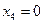 , оно не подходит
, оно не подходит
6) ответ: 3.
Ещё пример задания:
Дано логическое выражение, зависящее от 5 логических переменных:
z1 Ù z2 Ù z3 Ù z4 Ù z5
Сколько существует различных наборов значений переменных, при которых выражение ложно?
1) 1 2) 2 3) 31 4) 32
Решение:
1) задано выражение с пятью переменными, которые могут принимать 25 = 32 различных комбинаций значений
2) операция Ù– это логическое умножение, поэтому заданное выражение истинно только тогда, когда все сомножитель истинны, то есть в одном единственном случае
3) тогда остается 32 – 1 = 31 вариант, когда выражение ложно
4) ответ: 3.
Ещё пример задания:
Дан фрагмент таблицы истинности выражения F. Какое выражение соответствует F?
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | F |
1) (x1 Ú x2) Ù x3 Ù x4 Ù x5 Ù x6 Ù x7
2) (x1 Ù x2) Ú x3 Ú x4 Ú x5 Ú x6 Ú x7
3) (x1 Ù x2) Ù x3 Ù x4 Ù x5 Ù x6 Ù x7
4) (x1 Ù x2) Ù x3 Ù x4 Ù x5 Ù x6 Ù x7
Решение:
1) в последнем столбце таблицы всего одна единица, поэтому стоит попробовать использовать функцию, состоящую из цепочки операций «И» (ответы 1, 3 или 4);
2) для этой «единичной» строчки получаем, что инверсия (операция «НЕ») должна быть применена к переменным x3, x5 и x7, которые равны нулю:
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | F |
таким образом, остается только вариант ответа 1 (в ответах 3 и 4 переменная x3 указана без инверсии)
3) проверяем скобку (x1 Ú x2): в данном случае она равна 1, что соответствует условию
4) ответ: 1.
 Ещё пример задания:
Ещё пример задания:
Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z. Дан фрагмент таблицы истинности выражения F:
Какое выражение соответствует F?
1) X Ù Y Ù Z 2) X Ù Y Ù Z 3) X Ú Y Ú Z 4) X Ú Y Ú Z
Решение (основной вариант):
1) нужно для каждой строчки подставить заданные значения X, Y и Z во все функции, заданные в ответах, и сравнить результаты с соответствующими значениями F для этих данных
2) если для какой-нибудь комбинации X, Y и Z результат не совпадает с соответствующим значением F, оставшиеся строчки можно не рассматривать, поскольку для правильного ответа все три результата должны совпасть со значениями функции F
3) перепишем ответы в других обозначениях:
1) 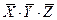 2)
2) 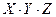 3)
3) 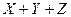 4)
4) 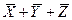
4) первое выражение, 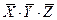 , равно 1 только при
, равно 1 только при 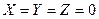 , поэтому это неверный ответ (первая строка таблицы не подходит)
, поэтому это неверный ответ (первая строка таблицы не подходит)
5) второе выражение, 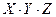 , равно 1 только при
, равно 1 только при 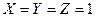 , поэтому это неверный ответ (первая и вторая строки таблицы не подходят)
, поэтому это неверный ответ (первая и вторая строки таблицы не подходят)
6) третье выражение, 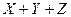 , равно нулю при
, равно нулю при 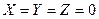 , поэтому это неверный ответ (вторая строка таблицы не подходит)
, поэтому это неверный ответ (вторая строка таблицы не подходит)
7) наконец, четвертое выражение, 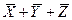 равно нулю только тогда, когда
равно нулю только тогда, когда 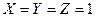 , а в остальных случаях равно 1, что совпадает с приведенной частью таблицы истинности
, а в остальных случаях равно 1, что совпадает с приведенной частью таблицы истинности
8) таким образом, правильный ответ – 4 ; частичная таблица истинности для всех выражений имеет следующий вид:
| X | Y | Z | F | 
| 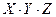
| 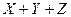
| 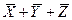
|
| 0 × | 0 × | ||||||
| – | – | 0 × | |||||
| – | – | – |
(красный крестик показывает, что значение функции не совпадает с F, а знак «–» означает, что вычислять оставшиеся значения не обязательно).
| Возможные ловушки и проблемы: · серьезные сложности представляет применяемая в заданиях ЕГЭ форма записи логических выражений с «закорючками», поэтому рекомендуется сначала внимательно перевести их в «удобоваримый» вид; · расчет на то, что ученик перепутает значки Ù и Ú (неверный ответ 1) · в некоторых случаях заданные выражения-ответы лучше сначала упростить, особенно если они содержат импликацию или инверсию сложных выражений (как упрощать – см. разбор задачи А10) |
Решение (вариант 2):
1) часто правильный ответ – это самая простая функция, удовлетворяющая частичной таблице истинности, то есть, имеющая единственный нуль или единственную единицу в полной таблице истинности
2) в этом случае можно найти такую функцию и проверить, есть ли она среди данных ответов
3) в приведенной задаче в столбце F есть единственный нуль для комбинации 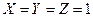
4) выражение, которое имеет единственный нуль для этой комбинации, это 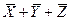 , оно есть среди приведенных ответов (ответ 4)
, оно есть среди приведенных ответов (ответ 4)
5) таким образом, правильный ответ – 4
| Возможные проблемы: · метод применим не всегда, то есть, найденная в п. 4 функция может отсутствовать среди ответов |
 Еще пример задания:
Еще пример задания:
Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z. Дан фрагмент таблицы истинности выражения F:
Какое выражение соответствует F?
1) X Ù Y Ù Z 2) X Ù Y Ù Z 3) X Ù Y Ù Z 4) X Ú Y Ú Z
Решение (вариант 2):
1) перепишем ответы в других обозначениях:
1) 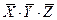 2)
2) 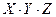 3)
3) 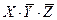 4)
4) 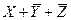
2) в столбце F есть единственная единица для комбинации 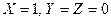 , простейшая функция, истинная (только) для этого случая, имеет вид
, простейшая функция, истинная (только) для этого случая, имеет вид 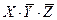 , она есть среди приведенных ответов (ответ 3)
, она есть среди приведенных ответов (ответ 3)
3) таким образом, правильный ответ – 3.
Еще пример задания:
Дано логическое выражение, зависящее от 5 логических переменных:
X1 Ù X2 Ù X3 Ù X4 Ù X5
Сколько существует различных наборов значений переменных, при которых выражение ложно?
1) 1 2) 2 3) 31 4) 32
Решение (вариант 2):
1) перепишем выражение в других обозначениях:
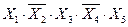
2) таблица истинности для выражения с пятью переменными содержит 25 = 32 строки (различные комбинации значений этих переменных)
3) логическое произведение истинно в том и только в том случае, когда все сомножители равны 1, поэтому только один из этих вариантов даст истинное значение выражения, а остальные 32 – 1 = 31 вариант дают ложное значение.
4) таким образом, правильный ответ – 3.
Ещё пример задания:
Дан фрагмент таблицы истинности выражения F.
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | F |
Какое выражение соответствует F?
1) x1 Ù x2 Ù x3 Ù x4 Ù x5 Ù x6 Ù x7
2) x1 Ú x2 Ú x3 Ú x4 Ú x5 Ú x6 Ú x7
3) x1 Ù x2 Ù x3 Ù x4 Ù x5 Ù x6 Ù x7
4) x1 Ú x2 Ú x3 Ú x4 Ú x5 Ú x6 Ú x7
Решение (вариант 2):
1) перепишем выражения 1-4 в других обозначениях:
1. 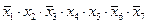
2. 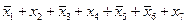
3. 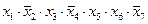
4. 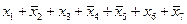
2) поскольку в столбце F есть два нуля, это не может быть выражение, включающее только операции «ИЛИ» (логическое сложение), потому что в этом случае в таблице был бы только один ноль, поэтому варианты 2 и 4 отпадают:
1. 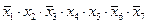
3. 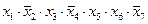
аналогично, если бы в таблице был один ноль и две единицы, это не могла бы быть цепочка операций «И», которая всегда дает только одну единицу;
3) для того, чтобы в последней строке таблицы получилась единица, нужно применить операцию «НЕ» (инверсию) к переменным, значения которых в этой строке равны нулю, то есть к 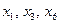 и
и  ; остальные переменные инвертировать не нужно, так как они равны 1; видим, что эти условия в точности совпадают с выражением 1, это и есть правильный ответ
; остальные переменные инвертировать не нужно, так как они равны 1; видим, что эти условия в точности совпадают с выражением 1, это и есть правильный ответ
4) Ответ: 1.