Из нормальной совокупности. Распределение Стьюдента.

 

Выборочное среднее, рассчитанное по конкретной выборке, есть конкретное число. Состав выборки случаен и среднее арифметическое, вычисленное по элементам другой выборки того же объёма, будет число отличное от первого.

- средняя арифметическая величина меняющаяся от выборки к выборке.

Теорема: Если случайная величина Х подчиняется нормальному закону с параметрами m и σ² Х(m, σ²), а х₁,х₂,х₃,…,х_n – это выборка из генеральной совокупности, то средняя арифметическая:

так же является случайной величиной подчиняющаяся нормальному закону с параметрами m и σ²/n, а нормированная случайная величина:

так же подчиняется нормальному закону с параметрами (0;1).

 

Пример. Автомат штампует детали, контролируется длина детали, которое подчиняется нормальному закону. Найти вероятность того, что средняя длина детали отобранных случайным образом отклонится от математического ожидания m на величину более чем 2 мм.

;

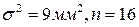
интеграл вероятности(функция Лапласса)

Предполагается при использовании таблиц интеграла вероятности, что объём выборки n достаточно велик(n ≥ 30).

Существует достаточно большое количество технических задач в которых не удаётся собрать выборку такого объёма. Тем не менее анализу такой выборки необходимо дать вероятностную оценку. Впервые такие задачи возникли в конце 19 века в области сельского хозяйства.

Агрономы опытных станций стояли перед дилеммой: либо нарезать на опытном поле побольше делянок с тем, чтобы увеличить повторность опыта или уменьшить количество делянок и использовать относительно большие поля.

В 1908 году английский математик Вильям Госсет дал решение задачи малых выборок (псевдоним Стьюдент). Стьюдент показал, что в условиях малых выборок надо рассматривать не распределение самих средних, а их нормированных отклонений от средних генеральных.

Надо рассматривать:

- это чётное распределение.

Оно зависит только от объёма выборки n и не зависит ни от математического ожидания, ни от дисперсии случайной величины Х. При n→∞ t – распределение Стьюдента переходит в нормальное распределение.

Поскольку в большинстве случаев σ генеральной совокупности неизвестно, то работают с такой величиной:

- это и есть состоятельная и несмещённая оценка.

Существуют t таблицы распределения Стьюдента.

Величина доверительной вероятности, её выбор находятся за пределами прикладной статистики. Они задаются самим исследователем. Величина доверительной вероятности определяется тяжестью тех последствий, которые могут произойти в случае, если произойдёт нежелательное событие.

Величина t_n,p показывает предельную случайную ошибку расхождения средневыборочного и математического ожидания.