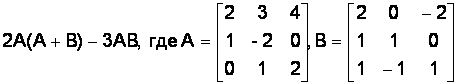Свойства транспонированных матриц.
1. Если E – единичная матрица, то E=ET.
2. Двукратное транспонирование не изменяет матрицу (AT)T = A.
3. Транспонирование суммы матриц равносильно сложению транспонированных матриц (A+B)T = AT+BT.
4. Транспонирование произведения матриц равносильно умножению транспонированных матриц: (AⅹB)T = AT ⅹBT .
5. Транспонирование обратной матрицы равносильно вычислению обратной к транспонированной матрице: (A-1)T = (AT)-1.
6. Если транспонированная матрица AT совпадает с данной матрицей A, то матрица A называется симметричной.
1.3. Обратная матрица
Матрица называется обратной к данной матрице A, если их произведение равно единичной матрице:
 .
.
Вырожденной квадратной матрицей называется такая матрица, определитель которой равен нулю.
Матрица, определитель которой не равен 0, называется невырожденной.
Для того, чтобы матрица A имела обратную матрицу, необходимо и достаточно, чтобы она была невырожденной. Для вычисления обратной матрицы к матрице А составим матрицу А* (присоединенную) из алгебраических дополнений матрицы А:
 .
.
Матрицу транспонируем и каждый элемент разделим на определитель |A|. Нетрудно показать, что построенная таким образом матрица будет обратной к матрице А [6]:
 .
.
F Пример 1.4. Дана матрица А. найти обратную матрицу при помощи MS Excel.
 .
.
@ Решение
В нашем случае матрица А находится в ячейках B1:D3. Для нахождения обратной матрицы необходимо вычислить матрицу, обратную к A. Для этого выделим ячейки для хранения обратной матрицы, пусть в нашем случае это будут ячейки G1:E3. Теперь обратимся к мастеру функций, и в категории Математические выберем функцию МОБР(), предназначенную для вычисления обратной матрицы (рис. 1.9), щелкнув по кнопке OK, перейдём ко второму шагу мастера функций.
В диалоговом окне, появляющемся на втором шаге мастера функций, необходимо заполнить поле ввода Массив (рис. 1.10). Это поле должно содержать диапазон ячеек, в котором хранится исходная матрица – в нашем случае B1:D3. Данные в поле ввода Массив можно ввести, используя клавиатуру или выделив их на рабочем листе, удерживая левую кнопку мыши.

Рис. 1.9. Мастер функций – шаг 1
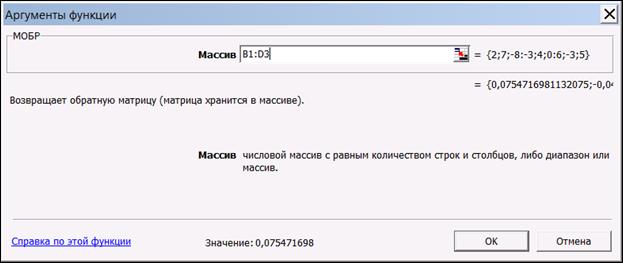
Рис. 1.10. Мастер функций – шаг 2
Если поле Массив заполнено, можно нажать кнопку OK. В первой ячейке, выделенного диапазона под обратную матрицу появится некое число. Чтобы получить всю обратную матрицу, необходимо нажать клавишу F2 для перехода в режим редактирования, а затем одновременно клавиши Ctrl+Shift+Enter. В нашем случае рабочая книга MS Excel примет вид, изображенный на рис. 1.11.

Рис. 1.11. Пример вычисления обратной матрицы
Для того чтобы проверить, правильно ли найдена обратная матрица, необходимо умножить матрицу Aна Аобр и получить в результате единичную матрицу. В результате проведенных вычислений рабочий лист примет вид, изображенный на рис. 1.12.

Рис. 1.12. Проверка правильности решения.
1.4. Сложение матриц
Суммой матриц A = (aij) и B(bij) одной и той же размерности (mⅹn) называется матрица того же размера C = (cij), каждый элемент которой представляет собой сумму соответствующих элементов матриц A и B:
C = A+B = (cij), где (cij) = (aij) + (bij), i = 1,…,m; j = 1,…,n,(1.3)
Матрицы разных размерностей складывать нельзя [6].
F Пример 1.5. Сложить матрицы А и В при помощи MS Excel.
 .
.
@ Решение
Введем исходные данные на рабочий лист. Для сложения матриц А и B выделим диапазон E4:F5 и введем формулу =B1:C2+F1:G2(рис. 1.13). Вычитание матриц выполняется аналогично. Для получения результата в обоих случаях необходимо нажать комбинацию клавиш Ctrl+Shift+Enter.

Рис. 1.13. Пример сложения матриц
Свойства сложения матриц:
A+B = B+A.
(A+B) + C = A + (B+C).
Если О – нулевая матрица размера mⅹn, то A+O = A; A+(-A) = O.
Матрица С = А+(-В) называется разностью матриц А и В и записывается в виде С = А-В [7].
Мы видим, что квадратные матрицы порядка n можно складывать, вычитать и перемножать.
1.5. Вычисление определителей
Пусть A = (aij) (i, j = 1, …, n) – квадратная матрица порядка n. Определителем (или детерминантом) матрицы A называется число, которое ставится в соответствие этой матрице и может быть вычислено по ее элементам. Простейший пример использования детерминанта – выяснение возможности обращения матрицы исходя из значения ее детерминанта. Если детерминант матрицы равен нулю, обратить ее невозможно.
Операция вычисления детерминанта определена только для квадратных матриц. Определители являются основными числовыми характеристиками квадратных матриц [7].
Определителем (детерминантом) матрицы A=(a11), состоящей из одного числа a11, называется само это число.
Определителем матрицы  второго порядка называется число, равное разности произведений элементов главной и побочной диагоналей:
второго порядка называется число, равное разности произведений элементов главной и побочной диагоналей:
 .
.
Рассмотрим матрицу третьего порядка:
 .
.
Определителем матрицы A третьего порядка называется число
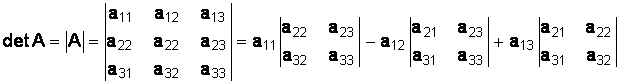 .
.
Данная формула называется формулой разложения определителя
3-го порядка по элементам первой строки [6].
Для вычисления детерминанта матрицы в Excel используется функция массива МОПРЕД().
F Пример 1.6. Вычислить определители заданных матриц:
1.6.1.  .
.
Решение :
 .
.
1.6.2. 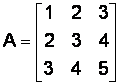 .
.
Решение:
 .
.
1.6.3.  .
.
Решение:
 .
.
@ Решение
Решим примеры при помощи пакета MS Excel. Матрица А находится в ячейках B1:C2. Для нахождения определителя матрицы необходимо перейти в свободную ячейку и обратиться к Мастеру функций. В категории Математические выберем функцию МОПРЕД(), предназначенную для вычисления определителя матрицы (рис. 1.14), щелкнув по кнопке OK, перейдём ко второму шагу мастера функций.
В диалоговом окне, появляющемся на втором шаге мастера функций, необходимо заполнить поле ввода Массив (рис. 1.15) Это поле должно содержать диапазон ячеек, в котором хранится исходная матрица, в нашем случае B1:С2.
Если поле Массив заполнено, можно нажать кнопку OK. В ячейке, выделенной под определитель матрицы, появится решение для первого примера, что соответствует представленному решению примера 1.6.1 (рис. 1.16).


Рис. 1.15. Мастер функций – шаг 2

Рис. 1.16. Вычисления определителя для примера 1.6.1
Аналогично проводим вычисления для примеров 1.6.2 и 1.6.3 (рис. 1.17 и 1.18). Применяя пакет MS Excel, сделаем проверку уже решенным примерам.
1.6.2.
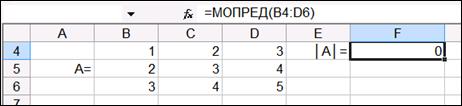
Рис.1.17. Вычисления определителя для примера 1.6.2
1.6.3.

Рис. 1.18. Вычисления определителя для примера 1.6.3
Определитель n-го порядка.
Определителем квадратной матрицы порядка n называется число:
 .
.
Свойства определителей.
ВАРИАНТЫ
Вариант № 1

Вариант № 2

Вариант № 3

Вариант № 4

Вариант № 5
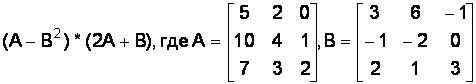
Вариант № 6

Вариант № 7

Вариант № 8
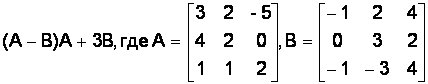
Вариант № 9

Вариант № 10

Вариант № 11

Вариант № 12

Вариант № 13

Вариант № 14

Вариант № 15
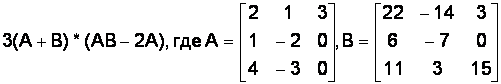
Вариант № 16

Вариант № 17

Вариант № 18

Вариант № 19
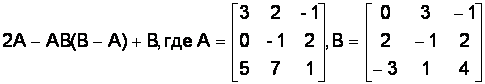
Вариант № 20

Вариант № 21

Вариант № 22

Вариант № 23
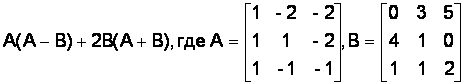
Вариант № 24

Вариант № 25

Вариант № 26
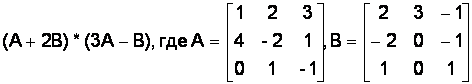
Вариант № 27
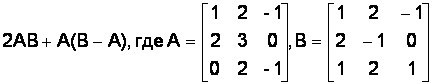
Вариант № 28

Вариант № 29