Задание
Выполнить действия над матрицами:
вычислить:
· обратную матрицу (А) с проверкой;
· определитель матрицы А;
· произведение матриц (А и В);
· выражение по формуле;
транспонировать матрицу В.
Пример 1.1. Вычислить произведение двух матриц А и В при помощи MS Excel.
 .
.
Введём матрицы A и В на рабочий лист MS Excel (рис. 1.1).

Рис. 1.1. Ввод матриц на рабочий лист
@ Решение
В нашем случае матрица А находится в ячейках B1:C3, а матрица В в диапазоне F1:H2.
Выделим ячейки для хранения результирующей матрицы, например D5:F7. Обратимся к мастеру функций, и в категории Математические выберем функцию МУМНОЖ()(рис. 1.2), которая предназначена для умножения матриц.
Напомним, что умножение матриц происходит по правилу строка на столбец и матрицу А можно умножить на матрицу В только в том случае, если количество столбцов матрицы А равно количеству строк матрицы В. Кроме того, при умножении матриц важен порядок сомножителей, т.е. АВ ≠ ВА.

Рис. 1.2. Мастер функций – шаг 1
Перейдём ко второму шагу мастера функций. Появившееся диалоговое окно (рис. 1.3) содержит два поля ввода Массив1 и Массив2. В поле Массив1 необходимо ввести диапазон ячеек, в котором содержится первая из перемножаемых матриц, в нашем случае B1:C3, а в поле Массив2 – ячейки, содержащие вторую матрицу, в нашем случае F1:H2.

Рис.1 3. Мастер функций – шаг 2
Если поля ввода заполнены, можно нажать кнопку OK. В первой ячейке выделенного диапазона появится соответствующее число результирующего вектора. Для того чтобы получить весь вектор, необходимо нажать клавишу F2, а затем одновременно клавиши Ctrl+Shift+Enter. В нашем случае результаты вычислений – матрица С, находится в ячейках B5:D7(рис.1.4).
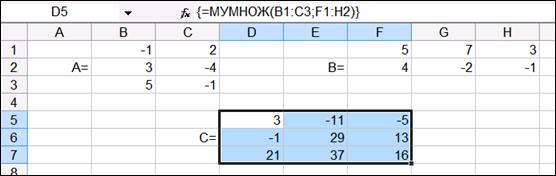
Рис. 1.4. Результат вычислений
Матрица C, элементы которой Сij равны элементам матрицы A, умноженным на число α, называют произведением матрицы A на a:
C = a A; ci,j = a aij; I = 1, …, m; j = 1, …, n, (1.2)
F Пример 1.2. Вычислить матрицу С по формуле: C = A2+2AB, где

@ Решение
Введем исходные данные на рабочий лист (рис. 1.5).
Для умножения матрицы Ана матрицу В выделим диапазон B5:D7и воспользуемся функцией МУМНОЖ(B1:D3;G1:I3).
Результат вычисления A2=A*Aпоместим в ячейки G5:I7, воспользовавшись формулой МУМНОЖ(B1:D3;B1:D3).
Умножение (деление) матрицы на число можно выполнить при помощи элементарных операций. В нашем случае необходимо умножить матрицу из диапазона B5:D7на число 2. Выделим ячейки B9:D11и введем формулу =2*B5:D7.
Сложение (вычитание) матриц выполняется аналогично. Например, выделим диапазон G9:I11и введем формул =B9:D11+ G5:I7.
Для получения результата в обоих случаях необходимо нажать комбинацию клавиш Ctrl+Shift+Enter.
Кроме того, в строке формул рабочего листа, изображенного на рис. 1.5, показано, как можно вычислить матрицу С одним выражением.

Рис. 1.5. Пример вычисления выражения 2-мя способами
Свойства умножения матрицы на число:
1. (A·B)·C = A·(B· C);
2. A·(B + C) = A·B + A ·C;
3. А·(В+С)=АВ+АС.
1.2. Транспонирование матриц
Матрица B = (bij) размера n×m называется транспонированной по отношению к матрице A = (aij) размера m ×n, если имеет вид bij = aji, т.е. A=(aij), Aт=B=(aji), i=1,…,m; j=1,…,n. Транспонированная матрица обозначается символом AT [7].
 .
.
F Пример 1.3. Дана матрица А. Транспонировать матрицу А при помощи MS Excel.
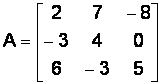 .
.
@ Решение
В нашем случае матрица А находится в ячейках B1:D3. Для транспонирования матрицы необходимо выделить ячейки для хранения транспонированной матрицы, пусть в нашем случае это будут ячейки G1:E3. Теперь обратимся к мастеру функций, и в категории ССЫЛКИ И МАССИВЫ выберем функцию ТРАНСП() (рис. 1.6), щелкнув по кнопке OK, перейдём ко второму шагу мастера функций.
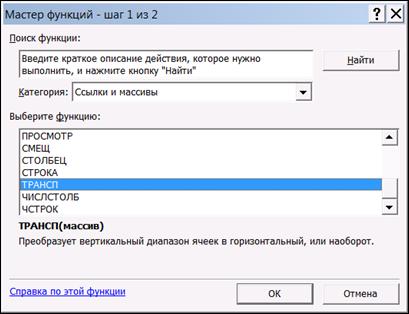
Рис. 1.6. Мастер функций – шаг 1
В диалоговом окне, появляющемся на втором шаге мастера функций, необходимо заполнить поле ввода Массив (рис. 1.7). Это поле должно содержать диапазон ячеек, в котором хранится исходная матрица – в нашем случае B1:D3. Данные в поле ввода Массив можно ввести, используя клавиатуру или выделив их на рабочем листе, удерживая левую кнопку мыши.
Если поле Массив заполнено, можно нажать кнопку OK. В первой ячейке, выделенного диапазона под транспонированную матрицу появится некое число. Для того чтобы получить всю матрицу, необходимо нажать клавишу F2 для перехода в режим редактирования, а затем одновременно клавиши Ctrl+Shift+Enter. В нашем случае рабочая книга MS Excel примет вид, изображенный на рис. 1.8.
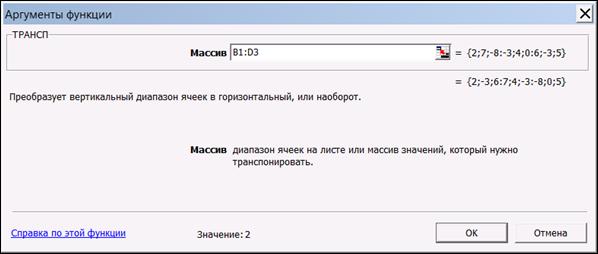
Рис. 1.7. Мастер функций – шаг 2

Рис.1.8. Пример вычисления транспонированной матрицы