КОРИСНІСТЬ ЗА НЕЙМАНОМ. СПОДІВАНА КОРИСНІСТЬ
Для визначення корисності розглянемо вибір особи за умов ризику, який формалізується за допомогою поняття лотереї.
Для этого необходимо из множены предосталенных экспертам значений экономического показателя (объекта) выделить два х* и х* таких, которые х*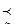 
х для всех х* 
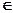Х и х* 
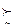х для всех х 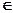Х, тобто найменш пріоритетне, в певному сенсі, значення економічного показника (це буде «нуль» даної шкали інтервалів) і найбільш пріоритетне у певному сенсі значення показника (разом з «нулем» воно визначить масштаб даної шкали). Власне так побудована функція корисності Дж. Неймана і О. Моргенштерна [32]. Експерту пропонують порівнювати альтернативу:
1) значення показника "х";
2) лотерею: одержати "х*" з імовірністю (1 - р) чи "х*" з імовірністю (р). Величину імовірності р змінюють доти, доки, на погляд експерта, значення показника "х" і лотерея L (х*, р, х*) не стануть еквівалентними. Максимальному та мінімальному значенням "х*" та "х*" приписують довільні числові значення U*= U(х*) та U*= U(x*), але так, щоб U* > U*.
Пiд лотереєю L (х*, р (х), х*) розуміють ситуацію, в якій особа може отримати "х*" з імовірністю "р"(х) або х* з імовірністю 1 - р(х).
Корисність варіанту "х" визначається ймовірністю р (х), при якій особі байдуже, що обирати: "х" — гарантовано, чи лотерею L (х*, р(х), х*), де "х*", "х*" — вектори, більш та менш пріоритетні порівняно з "х".
Нехай L — лотерея, що приводить до виграшів (подій) х1,х2,....хn з відповідними ймовірностями р1, p2, ….рN. Позначимо сподіваний виграш (математичне сподівання виграшу) через "х".
(3.14)
Справедлива главная формула теории ожидаемой полезности
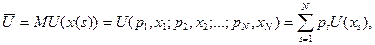(3.15)
тобто корисність ансамблю результатів збігається математичним сподіванням корисності результатів.
Поняття детермінованого еквівалента лотереї L є одним з основних при розгляді різних характеристик ризику і їх взаємозв'язку з функціями корисності.
Детерминованный эквивалент лотереи L – это гарантированная сумма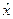 
, получение которой эквивалентна участию в лотереи, т.е. 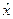~ L.
Следовательно 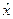определяется по уравнению:
U(x) = M [U(x)], или 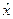= U [MU(x)]. (3.16)
Ожидаемый выигрыш и детерминованный эквивалент, определены по формулам (3.14) и (3.16), соответствуют лотереи с окончательным числом выигрышей. Если возможные выигрыши описываются щильностью распределения φ(х), то ожидаемый выигрыш в этой лотереи равняется:
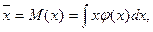(3.17)
а детерминованный эквивалент 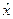является разрешением уравнения:
(3.18)
Пример. Пусть U(x) = a + bx, b > 0. Допустим, что особа, которая принимает решение, имеет дело с лотереей, которая имеет щильность распределения φ(х). Необходимо найти ожидаемый выигрыш и детерминованный эквивалент.
Решение. Ожидаемый выигрыш находим по формуле:
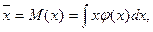
а детерминованный эквивалент 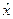является разрешением уравнения:
Поскольку U(x) = a + bx, то отсюда вытекает, что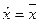 
. Этот пример показывает, что когда функция полезности является линейной, то детерминованный эквивалент какой-либо лотереи равна ожидаемому выигрышу этой лотереи.
Пример. Пусть U(x) = - be-cx, где b > 0. Допустим, что особа, имеет дело с лотереей 50 на 50 (т.е. с такой, что приводит с равными имоверностями или до х1, или до х2), обозначается как L(х1; 0,5; х2). Найти ожидаемый выигрыш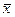 
и детерминованный эквивалент .
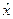Решение. Ожидаемый выигрыш 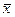равен (х1 + х2)/2. Детерминованный эквивалент находят из разрешения уравнения 
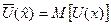, или из равнозначного уравнения
-е-сх = -(е-сх1 + е-сх2)/2.
Пример. Имеем функцию полезности, как в предыдущем примере. Допустим, что лотерея описывается щильностью равномерного распределения:
 |
φ(х) = 
х1 ≤ х ≤ х2,