Действия над комплексными числами в алгебраической форме.

Действия над комплексными числами определяются таким образом, чтобы для частного случая действительных чисел эти операции совпадали с известными операциями над ними.

Пусть даны два комплексных числа в алгебраической форме:

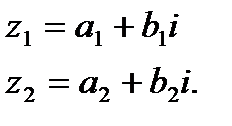
1. Суммой двух комплексных чисел z₁ и z₂ называется комплексное число

Т.е. чтобы сложить два комплексных числа, нужно сложить их действительные и мнимые части.

В частности сумма двух взаимно сопряженных комплексных чисел есть число действительное:

Пример. Найти сумму комплексных чисел

Решение:

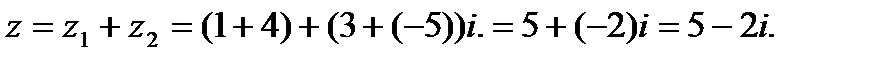
Операция сложения легко распространяется на сумму любого конечного числа комплексных чисел.

2. Вычитание двух комплексных чисел определяется как действие, обратное сложению. Разностью двух комплексных чисел z₁ и z₂ называется комплексное число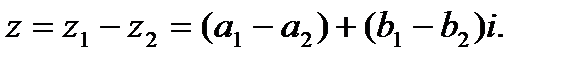

В частности разность двух взаимно сопряженных комплексных чисел есть число чисто мнимое: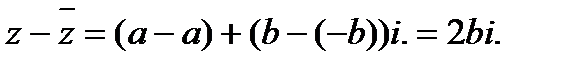

Пример. Найти разность комплексных чисел

Решение:

3. Произведением двух комплексных чисел z₁ и z₂ называется комплексное число

Умножение двух комплексных чисел подчиняется правилу умножения многочленов с учетом, что 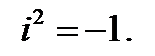Действительно,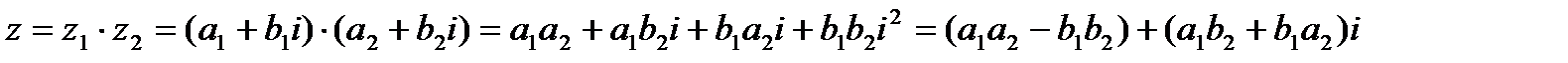

В частности произведение двух взаимно сопряженных чисел есть число действительное и равно сумме квадратов действительной части и коэффициента мнимой части комплексного числа:

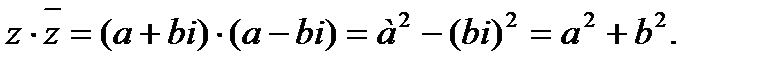
Пример. Найти произведение комплексных чисел

Решение:

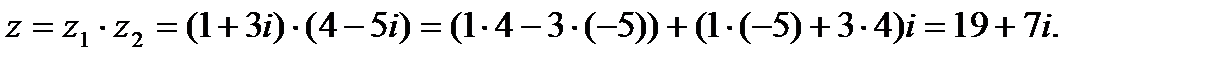
ИЛИ

4. Деление комплексных чисел определяется как операция обратная умножению. Частным двух комплексных чисел называется число

Тот же результат можно получить, умножив числитель и знаменатель дроби на число, сопряженное знаменателю:

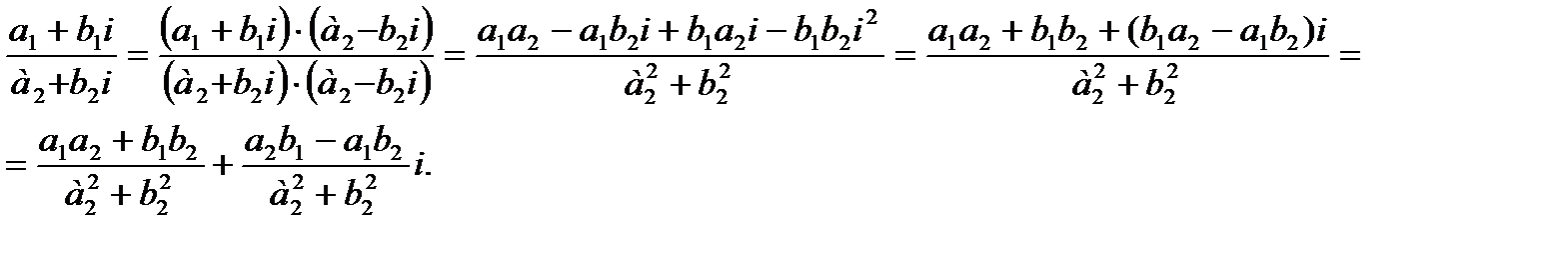
Пример. Найти частное комплексных чисел

Решение:

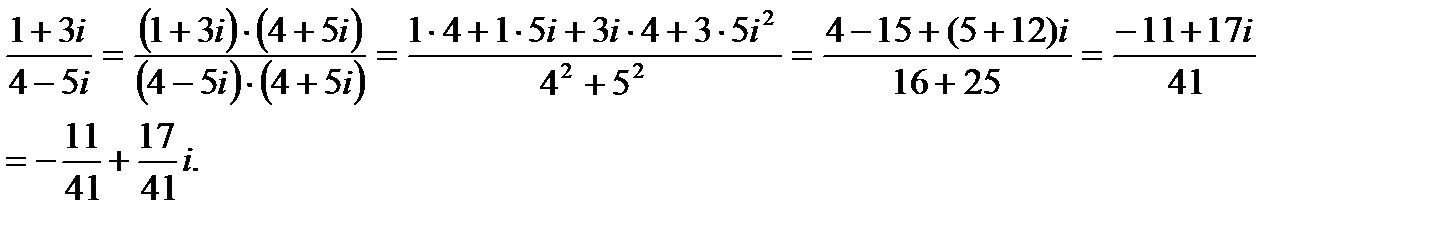
Действия над комплексными числами удовлетворяют основным законам сложения и умножения (коммутативность, ассоциативность, дистрибутивность). Однако, между комплексными числами не существует отношения порядка, т.е. понятий «больше» или «меньше».

5. Возведение комплексного числа в степень n 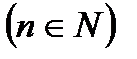рассматривается как частный случай умножения комплексных чисел:

n раз

 

Найдем натуральные степени мнимой единицы i: