Классическое определение вероятности. Теоремы сложения и умножения вероятностей

Число, характеризующее степень возможности наступления данного события, называется его вероятностью.

Рассмотрим такие эксперименты, в которых можно выделить конечное число «простых» событий, которые являются несовместными(два таких исхода не могут произойти одновременно), равновозможными(по условиям эксперимента нет оснований считать, что какие-либо их них будут происходить чаще, чем другие) и образуют полную группу(эти события являются единственно возможными и несовместными исходами испытания). Такие события назовем элементарными событиями (исходами, случаями).

Пусть 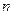– число возможных исходов данного опыта, – число его исходов, при которых происходит событие (назовем такие исходы благоприятствующими событию). Тогда вероятность события определяется как отношение числа благоприятствующих исходов к числу всех возможных исходов:

. (2.1)

Пример 8.Набирая номер телефона, абонент забыл одну цифру и набрал ее наудачу. Найдите вероятность того, что набрана нужная цифра.

Решение. Обозначим через событие – набрана нужная цифра. Абонент мог набрать любую из 10 цифр, поэтому общее число возможных элементарных исходов равно 10. Эти исходы несовместны, равновозможны и образуют полную группу. Благоприятствует событию А лишь один исход (нужная цифра лишь одна). Искомая вероятность равна отношению числа исходов, благоприятствующих событию, к числу всех элементарных исходов:

Пример 9.В урне находятся 25 белых и 5 черных шаров. Из урны наудачу извлекаются 9 шаров. Найдите вероятность того, что среди девяти извлеченных шаров имеется хотя бы один шар черного цвета.

Решение. Всего в урне 30 шаров. Будем считать, что все они пронумерованы. Эти 30 шаров разделяются на две группы. Первая группа состоит из 25-ти белых шаров, вторая группа состоит из 5-ти черных шаров. Эксперимент состоит в изъятии наудачу 9-ти шаров из 30-ти шаров (их порядок не имеет значения). Элементарным событием в этом эксперименте является любое сочетание из 30-ти элементов по 9. Тогда число таких элементарных событий равно:

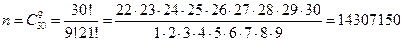Событие A – среди девяти вынутых шаров имеется хотя бы один черный шар. Событие означает, что нет ни одного черного шара среди вынутых, т. е. все 9 шаров – белые.

;

Поэтому .

Пример 10.В лотерее 2000 билетов. На один билет падает выигрыш 100 руб., на четыре билета – выигрыш по 50 руб., на десять билетов – выигрыш по 20 руб., на двадцать билетов – выигрыш по 10 руб., на 165 билетов – выигрыш по 5 руб., на 400 билетов – выигрыш по 1 руб. Остальные билеты невыигрышные. Какова вероятность выиграть по билету не менее 10 руб.?

Решение:

Здесь 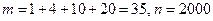, т. е. .

Вероятность суммы двух событий можно найти по теореме сложения вероятностей:

.(2.2)

Если события А и В несовместны, то есть не могут произойти одновременно, то вероятность их произведения равна нулю, и теорема сложения приобретает более простой вид:

. (2.3)

Вероятность произведения событий определяется по теореме умножения вероятностей:

, (2.4)

где – так называемая условная вероятность события В, то есть вероятность В при условии, что А произошло.

Если осуществление события А не изменяет вероятности события В, то А и В называются независимыми, и вероятность их произведения равна произведению вероятностей сомножителей:

. (2.5)

Пример 11.Два стрелка стреляют по одной мишени. Вероятности попадания в мишень при одном выстреле для стрелков соответственно равны p1 = 0,7 и p2 = 0,8. Найдите вероятность того, что при одном залпе в мишени будет: а) одно попадание; б) не менее одного попадания.

Решение. Случайные события: A – в мишени одно попадание,
B – в мишени не менее одного попадания. Введем случайные события:
C1 – в мишень попал первый стрелок, C2 – в мишень попал второй стрелок. Тогда

а) .

В формуле случайные события-слагаемые несовместны, а случайные события-сомножители независимы, так как вероятность попадания в мишень каждого из стрелков не зависит от результата другого стрелка. Поэтому

б) событие B равно: .

Поэтому

Вероятность события B можно найти также, вычислив сначала вероятность противоположного события . Т. к. ,
то .

Тогда .

По теореме умножения для трех событий получаем формулу:

Эту формулу можно обобщить и для n событий.

Пример 12.В библиотеке на стеллаже в случайном порядке расставлены десять учебников по экономике и пять – по математике. Библиотекарь наудачу берет три учебника. Найдите вероятность того, что: а) все три учебника по математике; б) хотя бы один из взятых учебников будет по математике.

Решение. Введем события А – все три учебника по математике,
В – хотя бы один из взятых учебников будет по математике, – учебник по математике, .

а) Тогда, . События зависимы. Значит вероятность события равна:

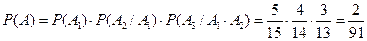б) Рассмотрим противоположное событие к событию В. Запишем событие .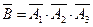

;

Пример 13.Абонент забыл последнюю цифру номера телефона и набирает ее наудачу. Вычислите вероятность того, что он наберет нужный номер не более чем за три попытки.

Решение. Случайное событие A – абонент дозвонился не более чем за три попытки набора номера. Пусть случайное событие Ai – абонент дозвонился при i-м наборе номера (i = 1, 2, 3).

Вероятность события A можно найти, вычислив сначала вероятность противоположного события и используя формулу .

Случайное событие – абонент не дозвонился за три набора номера – есть произведение трех событий: 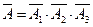, поэтому

Но тогда, .

Пример 14.ой кости, вторым – число очков, выпавших на второй кости; далее найдена сумма очков):

1) 6, 2; 6 + 2 = 8; 2) 6, 4; 6 + 4 = 10; 3) 6, 6; 6 + 6 = 12; 4) 2, 6; 2 + 6 = 8;
5) 4, 6; 4 + 6 = 10.

Искомая вероятность равна отношению числа исходов, благоприятствующих событию, к числу всех возможных элементарных исходов:

Пример 15.Найдите вероятность того, что при бросании трех игральных костей шестерка выпадет на одной кости, если на гранях двух других костей выпадут числа очков, не совпадающие между собой и не равные шести.

Решение. Общее число элементарных исходов испытания по правилу умножения равно: .

Число исходов, благоприятствующих появлению шестерки на одной грани и различного числа очков (не равного шести) на гранях двух других костей, равно: .

Искомая вероятность равна отношению числа исходов, благоприятствующих интересующему нас событию, к общему числу возможных элементарных исходов: