Геометрические вероятности
Чтобы преодолеть недостатки классического определения вероятности, состоящий в том, что оно неприменимо к испытаниям с бесконечным числом исходов и статистической вероятности – неоднозначность значения вероятности, вводят геометрические вероятности – вероятности попадания точки в некоторую область (отрезок, часть плоскости и т.д.).
Пусть отрезок l составляет часть отрезка L. На отрезок L наугад поставлена точка. Это означает выполнение предположений: поставленная точка с равной вероятностью может оказаться в любой точке отрезка L, вероятность попадания точки на отрезок l пропорциональна длине этого отрезка и не зависит от его расположения относительно отрезка L. В этих предположениях вероятность попадания точки на отрезок l определяется равенством Р=Длина l/ Длина L.
Пример 1.38. На отрезок ОА длины L числовой оси Ох наугад поставлена точка В(х). Найти вероятность того, что меньший из отрезков ОВ и ВА имеет длину, большую L/3. Предполагается, что вероятность попадания точки на отрезок пропорциональна длине отрезка и не зависит от его расположения на числовой оси.
Решение. Разобьем отрезок ОА точками С и D на 3 равные части. Требование задачи будет выполнено, если точка В(х) попадет на отрезок CD длины L/3. Искомая вероятность Р=( L/3)/ L = 1/3.
Пусть плоская фигура g составляет часть плоской фигуры G. На фигуру G наугад брошена точка. Это означает выполнение следующих предположений: брошенная точка с равной вероятностью может оказаться в любой точке фигуры G, вероятность попадания брошенной точки на фигуру g пропорциональна площади этой фигуры и не зависит ни от ее расположения относительно G, ни от формы g. В этих предположениях вероятность попадания точки в фигуру g определяется равенством
Р = Площадь g/ Площадь G.
Пример 1.39. На плоскости начерчены две концентрические окружности, радиусы которых 5 и 10 см, соответственно. Найти вероятность того, что точка, брошенная наугад в большой круг, попадет в кольцо, образованное построенными окружностями. Предполагается, что вероятность попадания точки в плоскую фигуру, пропорциональна площади этой фигуры и не зависит от ее расположения относительно большого круга.
Решение.
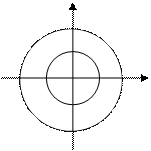 Площадь кольца (фигуры g)
Площадь кольца (фигуры g)
|
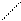
 Площадь большого круга (фигуры G)
Площадь большого круга (фигуры G)
SG = π102 = 100 π
|
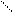
 Р = Sg/ SG =(75 π)/(100π) = 0,75.
Р = Sg/ SG =(75 π)/(100π) = 0,75.
Пример 1.40. Ромео и Джульетта договорились встретиться в определенном месте между двенадцатью и часом дня. Необходимо определить вероятность встречи, если приход каждого из них в течение указанного часа происходит случайным образом, причем известно, что Ромео ждет Джульетту ровно 20 минут, а Джульетта Ромео- 5 минут.
Решение. Воспользуемся геометрической схемой вероятности. Обозначим момент прихода Ромео через х, а Джульетты – через у. Тогда любой элементарный исход ω можно отождествить с некоторой точкой на плоскости хОу. Выберем за начало отсчета 12 часов, а за единицу измерения 1 минуту и построим на плоскости хОу пространство элементарных исходов Ω. Очевидно, что это квадрат G со стороной 60.
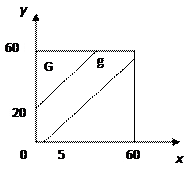 Событие А (Ромео и Джульетта встретятся) произойдет тогда, когда разность у-х не превысит t1 =20, а разность х-у не превысит t2 =5, т.е. условие встречи определяет систему неравенств у-х ≤ 20;
Событие А (Ромео и Джульетта встретятся) произойдет тогда, когда разность у-х не превысит t1 =20, а разность х-у не превысит t2 =5, т.е. условие встречи определяет систему неравенств у-х ≤ 20;
х-у ≤ 5.
Область элементарных исходов, благоприятствующих событию А представляет заштрихованную область g на рис.
Ее площадь равна площади квадрата без двух угловых треугольников, т.е.
SG = 602 = 3600
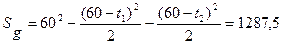
Тогда, согласно определению искомая вероятность равна