Задание

Определить с помощью метода Хука-Дживса точку минимума функций (вид функции согласно варианту задания, приведенного в таблице 1).

Исследование функций проводить с помощью программы, реализованной на языке DELPHI или BorlandС++.

 

Интерфейс программы должен также содержать:

- исследуемые функции;

- исходные данные для исследуемой функции (начальная точка , приращение по координатам , коэффициент уменьшения шага , точность вычисления );

- окно промежуточных результатов: номер итерации, приращение по координатам , координаты базовых точек и значения функции в этих точках);

- окно окончательных результатов ( 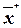и ;

- поле с линиями равного уровня целевой функции.

 

Таблица 1.

Целевые функции

 

Номер варианта	Вид целевой функции
	(x+1)2+x×y+(y-2)2
	(x+1)2+x2×y+(y-3)2
	(10×x-5)2+0,2×(y-2)2
	10×(x×y-5)2+(y-5)2
	x2+0,5×x2×y2+x+(y-5)2
	x2+0,5×x2×y2+x+y2
	x2+5×x2×y2-y+(y-5)2
	15×x2+4×x2×y2+10×(y-2)2
	2×x2+5×(x+y)2+10×(y-2)2
	0,5×x2+x2×(x-y)2+0,5×(y-2)2
	2×x2+x2×(x+5)2+0,5×(y+2)2
	(x-2)2+y2×(x-5)2+0,5×(y+1)2
	5×(x-2)2+(5×x+2×y)2+0,5×(y+1)2
	(x-2)2+x×y2+2×(y-1)2
	(2×x-3)2+5×x×y2+2×(y-2)2
	(1,2×x-3)2+3×x×y2+2×(y+2)2
	(0,6×x-3)2+0,2×x2×y+4×(y-2)2
	x2+x2×y+y2+5
	x2+(x+2)2+2×y2+10
	x2×(y+1)2+(y-1)2+1
	(15×x-y)2+(5-y)2
	(x-0,1×y)2+(5-y)2
	(x-2)2+x+y+y2
	(x+1)2+(y-0,2×x)2
	5×(x-0,2×y)2+(0,5×y+2)2