Теоретические сведения, необходимые для выполнения работы

В косозубом колесе различают нормальный m_n и окружной m_t модули. Эти модули связаны зависимостью: ,

где β =18º– угол наклона линии зуба на делительном цилиндре (для данного редуктора).

По стандарту для колеса, нарезанного без смещения, принимается:

Высота головки зуба - h_a=1∙m_n

Высота ножки зуба - h_f=1,25∙m_n

Радиальный зазор - с=0,25∙m_n

Угол исходного контура α=20º,

cos 20°=0,939693; sin 20°=0,342020; tg 20°=0,363970; inv 20°= 0,014904384

Определение нормального модуля через межосевое расстояние и диаметры выступов :

m_n=(d_a₁+d_a₂-2·a_w)/4

Вычисляем значение нормального модуля через высоту зуба: m_n = h_зуба/(1+1,25+0,25);

Нормальный модуль регламентируется по ГОСТ 9563-60. Извлечение из этого стандарта:

I ряд - 1; 1, 25; 1, 5; 2; 2, 5; 3; 4; 5; 6; 8; 10…

II ряд - 1, 125; 1, 375; 1, 75; 2, 25; 2, 75; 3, 5; 4, 5; 5, 5; 7, 0; 9, 0…

Угол наклона линии зуба: cos β = m_n·(z₁+z₂)/2·a_w.

Торцевой модуль зуба

Делительные диаметры ; .

Диаметр вершин зубьев

Диаметр впадин зубьев

Межосевое расстояние ,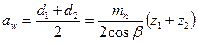

Коэффициент ширины зубчатого венца: ψ_а=b/a_w

Нормальный шаг: ;

Окружной шаг: ;

Осевой шаг:

Угол зацепления α_tw=α_t=arctg(tgα/cosβ), при х_Σ=0.

Основной угол наклона β_b=arcsin(sin β/cos α)

Длина общей нормали при обхвате

z_n₁ зубьев W₁=(π∙(z_n₁-0,5)+2∙x₁∙tgα+z₁∙inv(α_tw))∙m_n∙cos α

W₂=(π∙(z_n₂-0,5)+2∙x₂∙tgα+z₂∙inv(α_tw))∙m_n∙cos α

Принять: x₁=0, z_n₁=3…4; x₂=0, z_n₂=3…4; π=3,14159; tgα=0,363970; cos α=0,93969;

Приложение А

Рисунок 4. Картер редуктора цилиндрического

Рисунок 5 Вал шлицевый

Рисунок 6 Вал гладкий

Рисунок 7 Зубчатые колеса

Рисунок 8 Стакан и крышка подшипникового узла

Приложение Б

Образец оформления отчета