Выборочное наблюдение: понятие, виды, ошибки выборки, оценка результатов. Примеры решения задач

Как известно, в статистике существует два способа наблюдения массовых явлений в зависимости от полноты охвата объекта: сплошное и несплошное. Разновидностью несплошного наблюдения является выборочное наблюдение.

Под выборочным наблюдением понимается несплошное наблюдение, при котором статистическому обследованию (наблюдению) подвергаются единицы изучаемой совокупности, отобранные случайным образом.

Выборочное наблюдение ставит перед собой задачу – по обследуемой части дать характеристику всей совокупности единиц при условии соблюдения всех правил и принципов проведения статистического наблюдения и научно организованной работы по отбору единиц.

Совокупность отобранных для обследования единиц в статистике принято называть выборочной совокупностью, а совокупность единиц, из которых производится отбор, называют генеральной совокупностью. Основные характеристики генеральной и выборочной совокупности представлены в таблице 1.

Таблица 1 - Основные характеристики генеральной и выборочной совокупности
Показатель	Обозначение или формула
Генеральная совокупность	Выборочная совокупность
Число единиц	N	n
Число единиц, обладающих каким-либо признаком	M	m
Доля единиц, обладающих этим признаком	p = M/N	ω = m/n
Доля единиц, не обладающих этим признаком	q = 1 - p	1 - ω
Средняя величина признака
Дисперсия признака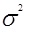
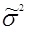
Дисперсия альтернативного признака (дисперсия доли)	pq	ω (1 - ω )

При проведении выборочного наблюдения возникают систематические и случайные ошибки. Систематические ошибки возникают в силу нарушения правил отбора единиц в выборку. Изменив правила отбора, от таких ошибок можно избавиться.

Случайные ошибки возникают в силу несплошного характера обследования. Иначе их называют ошибками репрезентативности (представительности). Случайные ошибки разделяют на средние и предельные ошибки выборки, которые определяются как при расчете признака, так и при расчете доли.

Средние и предельные ошибки связаны следующим соотношением:Δ = tμ, где Δ - предельная ошибка выборки, μ - средняя ошибка выборки, t - коэффициент доверия, определяемый в зависимости от уровня вероятности. В таблице 2 приведены некоторые значения t, взятые из теории вероятностей.

Таблица 2 - Соответствие некоторых значений вероятностей коэффициенту доверия
Вероятность, Р	0,683	0,866	0,954	0,988	0,997	0,999
Значение t	1,0	1,5	2,0	2,5	3,0	3,5

Величина средней ошибки выборки рассчитывается дифференцированно в зависимости от способа отбора и процедуры выборки. Основные формулы для расчета ошибок выборки представлены в таблице 3.

Таблица 3 - Основные формулы для расчета ошибок выборки при повторном и бесповторном отборе
Показатель	Обозначение и формула
Генеральная совокупность	Выборочная совокупность
Средняя ошибка признака при случайном повторном отборе
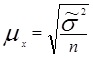
Средняя ошибка доли при случайном повторном отборе
Предельная ошибка признака при случайном повторном отборе
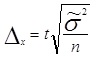
Предельная ошибка доли при случайном повторном отборе
Средняя ошибка признака при случайном бесповторном отборе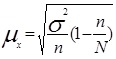
Средняя ошибка доли при случайном бесповторном отборе
Предельная ошибка признака при случайном бесповторном отборе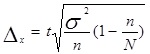
Предельная ошибка доли при случайном бесповторном отборе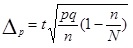

Расчет средней и предельной ошибок выборки позволяет определить возможные пределы, в которых будут находиться характеристики генеральной совокупности.

Например, для выборочной средней такие пределы устанавливаются на основе следующих соотношений:

- пределы доли признака в генеральной совокупности р.