Дифференциальное исчисление функций нескольких переменных.
Частной производной функции  по переменной
по переменной 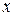 называется конечный предел
называется конечный предел  , т. е. чтобы найти частную производную
, т. е. чтобы найти частную производную  по
по 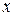 , надо
, надо 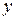 считать постоянной и руководствоваться обычными правилами и формулами дифференцирования.
считать постоянной и руководствоваться обычными правилами и формулами дифференцирования.
Аналогично определяется и производная  по
по 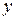 :
:  .
.
Пример 1.  . Найти
. Найти  и
и  .
.
Решение. Считаем 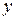 постоянной, тогда
постоянной, тогда  . Если
. Если 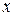 – постоянная, то
– постоянная, то  .
.
Пример 2.  . Найти
. Найти  и
и  .
.
Решение. Если 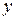 постоянная, то это степенная функция:
постоянная, то это степенная функция:  ; при постоянной
; при постоянной 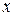 функция
функция  – показательная функция, тогда
– показательная функция, тогда  .
.
Частные производные второго порядка:
 ;
;  ;
;
 ;
;  .
.
Для большого класса функций смешанные производные равны, т.е.
 .
.
Пример 3. Убедиться, что смешанные производные функции  равны.
равны.
Решение.  ;
;  ,
,
 ;
;  .
.
Таким образом,  .
.
Пример 4. Показать, что функция  удовлетворяет уравнению
удовлетворяет уравнению  .
.
Решение. Находим  ;
;
 . Подставляем найденные выражения в левую часть уравнения
. Подставляем найденные выражения в левую часть уравнения 
 , что и требовалось.
, что и требовалось.
Ряды.
4.1. Знакоположительные числовые ряды.
Пусть дана бесконечная числовая последовательность  Выражение вида
Выражение вида  – называется числовым
– называется числовым
рядом, где  – общий член ряда.
– общий член ряда.
Сумму первых  членов ряда называют
членов ряда называют  - ой частичной суммой и обозначают
- ой частичной суммой и обозначают  .
.
Ряд называют сходящимся, если существует конечный предел последовательности частичных сумм, т.е.  . Число
. Число  называют суммой ряда. Если
называют суммой ряда. Если  или не существует, ряд называют расходящимся.
или не существует, ряд называют расходящимся.
Пример 1. Ряд, составленный из членов геометрической прогрессии сходится тогда и только тогда, когда  .
.
Доказательство. Дан ряд  ,
,  -ая частичная сумма
-ая частичная сумма  .
.
При  :
:  – ряд сходится. Если
– ряд сходится. Если  , то
, то  или не существует, ряд расходится. Итак,
или не существует, ряд расходится. Итак,  (
(  ).
).
Необходимый признак сходимости. Если ряд сходится, то  .
.
Таким образом, если  , то ряд расходится.
, то ряд расходится.
Пример 2. Покажем, что ряд  расходится.
расходится.
Решение.  – общий член ряда;
– общий член ряда;  , значит ряд расходится.
, значит ряд расходится.
Перечислим основные достаточные признаки сходимости рядов с положительными членами.
Первый признак сравнения. Пусть даны два ряда
 (1)
(1)
 , (2)
, (2)
причем каждый член ряда (1) не превосходит соответствующего члена ряда (2), т. е.  для всех
для всех  . Тогда, если сходится ряд (2), сходится и ряд (1), если расходится (1), то расходится (2).
. Тогда, если сходится ряд (2), сходится и ряд (1), если расходится (1), то расходится (2).
Второй признак сравнения. Если существует конечный и отличный от нуля предел  , то оба ряда (1) и (2) одновременно сходятся или одновременно расходятся.
, то оба ряда (1) и (2) одновременно сходятся или одновременно расходятся.
Признак Даламбера. Если для ряда  существует предел
существует предел  , то этот ряд сходится при
, то этот ряд сходится при  и расходится при
и расходится при  .
.
Пример 3.  сходится, так как
сходится, так как  ;
;  ,
, 
 .
.
Пример 4.  расходится, так как
расходится, так как  ;
;  ;
;
 .
.
Признак Коши. Если для ряда  существует
существует  , то при
, то при  ряд сходится, при
ряд сходится, при  расходится.
расходится.
Пример 5.  сходится, так как
сходится, так как  ;
;  ;
;
 .
.
Признак Дирихле. Ряд  сходится тогда и только тогда, когда
сходится тогда и только тогда, когда  .
.
Пример 6. Гармонический ряд  расходится, так как
расходится, так как  .
.
Пример 7. Ряд  сходится, так как
сходится, так как  .
.
Пример 8. Ряд  расходится, так как его можно сравнивать по второму признаку с гармоническим рядом, который расходится.
расходится, так как его можно сравнивать по второму признаку с гармоническим рядом, который расходится.
 ~
~  (при
(при  ).
).
Пример 9.  сходится, так как
сходится, так как  ~
~  , ряд
, ряд  сходится
сходится  , значит по второму признаку сравнения сходится и данный ряд.
, значит по второму признаку сравнения сходится и данный ряд.
4.2. Знакочередующиеся ряды. Для знакочередующего ряда

справедлив признак сходимости Лейбница: знакочередующийся ряд сходится, если абсолютные величины его членов монотонно убывают, а общий член стремится к нулю, т. е.
1)  ;
;
2)  .
.
Пример 10.  сходится, так как
сходится, так как
1)  ;
;  ;
;  , …, т. е.
, …, т. е.  ...;
...;
2)  .
.
Абсолютная и условная сходимость. Рассмотрим знакопеременный ряд 
и ряд, составленный из абсолютных величин членов исходного ряда:

Если сходится ряд  , то сходится исходный ряд и называется абсолютно сходящимся.
, то сходится исходный ряд и называется абсолютно сходящимся.
Сходящийся ряд  называют условно сходящимся, если ряд
называют условно сходящимся, если ряд  расходится.
расходится.
Пример 11.  сходится (по признаку Лейбница), а ряд
сходится (по признаку Лейбница), а ряд
 расходится
расходится  , значит, данный ряд сходится условно.
, значит, данный ряд сходится условно.
Пример 12.  сходится абсолютно, так как ряд
сходится абсолютно, так как ряд  сходится
сходится  .
.
4.2. Степенные ряды. Ряд вида

называется степенным. Числа  ,
,  , …,
, …,  ,… – коэффициенты ряда (действительные числа),
,… – коэффициенты ряда (действительные числа),  – центр ряда (также действительное число).
– центр ряда (также действительное число).
Теорема (об области сходимости степенного ряда). Для всякого степенного ряда существует интервал сходимости с центром в точке  :
:  , внутри которого степенной ряд абсолютно сходится и вне которого расходится.
, внутри которого степенной ряд абсолютно сходится и вне которого расходится.
На концах интервала  требуется дополнительное исследование.
требуется дополнительное исследование.
Радиус сходимости  можно находить по формуле:
можно находить по формуле:  .
.
Пример 13. Найти область сходимости степенного ряда
 .
.
Коэффициент n–го члена равен  ; коэффициент (n+1)–го члена
; коэффициент (n+1)–го члена  , следовательно
, следовательно  .
.
Таким образом, ряд абсолютно сходится для всех значений x из интервала  . Для значений
. Для значений  и
и  ряд расходится. Исследуем поведение ряда на концах интервала сходимости. Подставляем в заданный ряд
ряд расходится. Исследуем поведение ряда на концах интервала сходимости. Подставляем в заданный ряд  . Получаем числовой ряд
. Получаем числовой ряд  – этот ряд гармонический, он, как известно, расходится. При
– этот ряд гармонический, он, как известно, расходится. При  получаем ряд
получаем ряд  Этот знакопеременный ряд сходится, так как удовлетворяет условиям признака Лейбница.
Этот знакопеременный ряд сходится, так как удовлетворяет условиям признака Лейбница.
Итак, область сходимости степенного ряда определяется двойным неравенством  .
.