Дифференциальное исчисление функций одной переменной.

 

2.1. Производная функции.

Определение. Производной функции 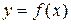называется предел отношения приращения функции к соответствующему приращению аргумента, когда приращение аргумента стремится к нулю:

 

.

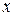Если этот предел конечный, то производная существует и функция называется дифференцируемой в точке . Производная обозначается также или . Процесс нахождения производной называется дифференцированием функции.

 

Правила дифференцирования функций.Пусть - постоянная, а , - функции, имеющие производные, тогда

1. .

2. = .

3. .

4. .

5. , .

6. Если функция 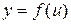дифференцируемая по , а функция по x, то сложная функция имеет производную (правило дифференцирования сложных функций).

 

Таблица производных элементарных функций

1. .

1а. . 1б. .

2. . 2а. .

3. . 3а. .

4. . 5. .

6. . 7. .

8. . 9. .

10. . 11. .

Пример 1. Используя правила дифференцирования и таблицу производных, найти производные следующих функций:

1) , 2) ,

3) , 4) ,

5) , 6) ,

7) .

Решение. 1) Перепишем данную функцию в виде: , тогда

.

2) Записываем данную функцию в виде степени: и вычисляем: .

3) Применив правило дифференцирования произведения (формула 4), находим:

.

4) Дифференцируя функцию как сложную находим производную:

.

5) По правилу дифференцирования частного (формула 5) получаем:

.

6) По аналогии с примером 3 находим:

.

7) Так как данная функция - показательная, то, согласно формуле 2

2.2. Производные высших порядка. Производной второго порядка (второй производной) от функции 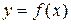называется производная от ее производной, т.е.

.

Вторую производную также обозначают или . Производная от производной второго порядка называется производной третьего порядка и т. д. Производную -го порядка обозначают или .

Пример 3. Найти вторую производную функции .

Решение. Найдем сначала первую производную функции

, тогда вторая производная .

 

2.3. Геометрические приложения производной.

Теорема.Если кривая задана уравнением , то значение производной в точке , равно угловому коэффициенту касательной к кривой в точке : , где (см. рис 9).

Уравнение касательной к кривой 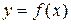в точке имеет вид:

или .

Определение. Углом между двумя кривыми в точке их пересечения называется угол между касательными к кривым в этой точке.

Угол между прямыми с угловыми коэффициентами и находится по формуле:

,

причем знак “плюс” соответствует острому углу θ, а знак “минус” – тупому.

Если , то касательные – взаимно перпендикулярны, а кривые называются ортогональными.

Пример3. Найти уравнение касательной к графику функции , которая параллельна прямой . Сделать чертеж.

Решение. График функции – парабола. Так как при , , то вершиной параболы является точка (2; –1). По условию, касательная к параболе и данная прямая , заданная уравнением , параллельны, значит, их угловые коэффициенты равны:

, ,

.

Следовательно, - абсцисса точки касания параболы и прямой , – ее ордината. Таким образом, уравнение касательной имеет вид:

или (см. рис.10).

 

2.4. Дифференцирование функции, заданной параметрически.

Если функция 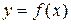задана параметрически двумя уравнениями , , , то ее производные вычисляются по формулам:

, .

Примечание. Производные по аргументу иногда, следуя Исааку Ньютону, обозначают точками наверху: , , . В этих обозначениях формулы, по которым находятся производные параметрически заданной функции, принимают вид:

, .

Пример 4. Найти и , если функция задана параметрически:

.

Решение. Последовательно находим: , ; ;

; , .

 

 

2.5. Дифференцирование неявной функции.

Говорят, что уравнение задает неявно функцию , на интервале , если для всех выполняется равенство .

Для вычисления производной функции следует продифференцировать по x тождество , помня, что 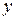есть функция от 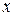, а затем полученное уравнение разрешить относительно .

Пример 5. Найти значение в точке для функции, заданной неявно уравнением .

Решение. Продифференцируем обе части уравнения по 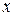(не забываем, что 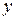зависит от ):

, ,

, .

 

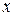2.6. Правило Лопиталя.

При раскрытии неопределенностей и , кроме классических методов вычисления пределов, рассмотренных ранее, во многих случаях можно пользоваться правилом Лопиталя-Бернулли: если или и существует предел отношения их производных , то .

Это правило справедливо и в случае .

Пример 6. .

 

Пример 7. .

Здесь мы дважды применили правило Лопиталя и воспользовались первым замечательным пределом.

Пример 8. .

При раскрытии неопределенностей и для применения правила Лопиталя данное выражение надо преобразовать в отношение двух функций (в неопределенность или ).

Пример 9. .

Пример 10.

.

 

При раскрытии неопределенностей , , рекомендуется найти предварительно предел логарифма искомой функции.

Пример 11. .

Решение. Введем обозначение , тогда .

. Так как .

 

2.7. Исследование функции и построение ее графика.

Для построения графика функции 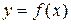сначала проводим элементарное исследование: находим область определения, асимптоты, выясняем некоторые особенности функции (если они имеются), т. е. точки пересечения с осями координат, симметрия, периодичность. Затем, используя первую производную, находим интервалы монотонности, экстремумы, а по второй производной – интервалы выпуклости, точки перегиба.

 

Пример 12. Построить график функции .

Решение. 1. Область определения данной функции: .

2. Пределы функции в точках разрыва и на концах области определения (данная функция имеет одну точку разрыва):

; ; .

3. Асимптоты. Если , то прямая – вертикальная асимптота. В нашем случае вертикальная асимптота имеет уравнение . Прямая является наклонной асимптотой, если существуют конечные пределы

и .

Так как ; , то наклонная асимптота имеет уравнение .

Если , то – горизонтальная асимптота.

4. Точки пересечения графика с осями координат дают: во-первых, нули функции (чтобы их найти, необходимо решить уравнение ) и, во-вторых, значение , если . Так как для данной функции , то график проходит через точку О .

5. Симметрия. Функция – четная, если ; ее график симметричен относительно оси 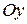. Функция – нечетная, если ; ее график симметричен относительно начала координат. В нашем случае

; ,

т. е. и , следовательно, симметрии относительно осей координат у графика нет.

6. Периодичность. Если для некоторого числа выполняется равенство для всех , то функция – периодическаяс периодом . Очевидно, наша функция не является периодической.

7. Первая производная: .

Находим критические точки, т.е. точки, в которых (стационарные точки) или не существует, имеем

,

производная не существует при .

Отметив их на области определения функции, получим интервалы знакопостоянства производной .

Определяем знак производной в каждом интервале. Там, где , функция возрастает ( ), а там, где , функция убывает ( ).

Результаты исследования сводим в таблицу:

 

(0; 1)
+ – – +

 

Экстремумы функции (максимум или минимум, если они есть):

.

8. Вторая производная: .

Находим критические точки второго рода, т.е. точки, в которых или не существует, имеем

, , производная не существует при .

Отметив их на области определения функции, получим интервалы знакопостоянства .

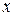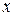Найдем промежутки выпуклости и вогнутости функции. Определяем знак производной в каждом интервале. Кривая является вогнутой при тех значениях аргумента , при которых (в окрестности точки вогнутости график располагается над касательной к нему в этой точке; в таблице интервал вогнутости будем обозначать символом ). Кривая в точке является выпуклой, если в этой точке (в этой точке график располагается под касательной и выпуклостью вверх ). Результаты сводим в таблицу:

 

+ – – +
точка перегиба

 
 

В окрестности точки вторая производная имеет разные знаки. Находим значение , тем самым определяем точку – точку перегиба.

9. Строим график (см. рис 11). При необходимости, находят несколько дополнительных точек.

Пример 13. Построить график функции .

Решение. 1. Область определения данной функции

.

2. ; , так как .

3. и — вертикальные асимптоты; — горизонтальная асимптота.

4. график не пересекает ось ;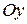

: ; ; , т.к. .

5 – 6. Нет.

7. для всех . Следовательно, функция возрастает на интервалах и .

8. ; имеет знак тот же, что и аргумент