Построение неявных схем
Для построения  -шаговой неявной (интерполяционной) схемы будем использовать интерполяционный многочлен Ньютона, построенный по значениям функции
-шаговой неявной (интерполяционной) схемы будем использовать интерполяционный многочлен Ньютона, построенный по значениям функции  в узлах
в узлах  :
:
 ,
,
где
 ,
,
 ,
,
............................................

Воспользуемся формулой
 .
.
Подставляя в эту формулу интерполяционный многочлен, получим общий вид неявной схемы Адамса:
 ,
,
где коэффициенты  имеют новый смысл:
имеют новый смысл:
 , т.е.
, т.е.  , и т.д.
, и т.д.
В частности, полагая  , получим двухшаговую неявную схему Адамса:
, получим двухшаговую неявную схему Адамса:
 (19)
(19)
4.9.2. Двухшаговая схема: погрешность аппроксимации
и устойчивость на модельной задаче
Аналогично разделу 3.8.2., определим порядок аппроксимации неявной двухточечной семы Адамса (19). Погрешность аппроксимации запишется следующим образом:
 ,
,
где
 ,
,
 - точное решение задачи Коши.
- точное решение задачи Коши.
Тогда справедливы следующие разложения:
 ,
,
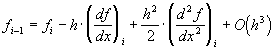 ,
,
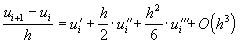 .
.
С учетом этих разложений формула для погрешности аппроксимации примет вид
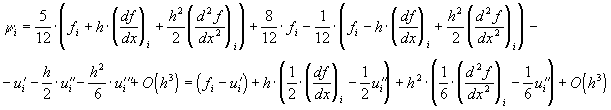
Однако очевидно, что 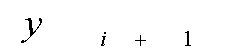 , поэтому для погрешности аппроксимации получаем соотношение
, поэтому для погрешности аппроксимации получаем соотношение 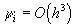 , а значит, двухточечная неявная схема Адамса имеет порядок аппроксимации, равный трем.
, а значит, двухточечная неявная схема Адамса имеет порядок аппроксимации, равный трем.
Исследуем устойчивость схемы (19) на модельной задаче
 ,
,  ,
,  .
.
Для этой задачи схема (19) примет конкретную форму трехточечного разностного однородного уравнения с постоянными коэффициентами:
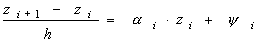 .
.
Подставляя в это уравнение частное решение вида 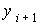 , получим квадратное уравнение для
, получим квадратное уравнение для 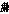 :
:
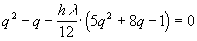
или
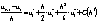 ,
,
где 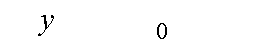 . Поскольку
. Поскольку 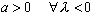 , можно записать неравенство для корней квадратного уравнения:
, можно записать неравенство для корней квадратного уравнения:
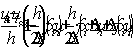 .
.
В силу последнего неравенства, если выполнены условия 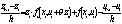 , то
, то
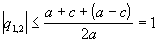 .
.
Это значит, что для устойчивости разностной схемы достаточно выполнения неравенства
 ,
,
что равносильно ограничению на шаг разностной схемы 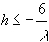 .
.