Алгоритм на псевдокоде
Поиск элемента с ключом X
L: = 1, R: =n
DO (L<R)
m: = 
IF (am < X) L: = m+1
ELSE R: = m
FI
OD
IF (ar=X) Найден: =да
ELSE Найден: =нет
FI
Нетрудно заметить, что после выхода из цикла L = R. Если в массиве несколько элементов с одинаковым ключом, то эта версия алгоритма находит самый левый из них. Для поиска остальных элементов с заданным ключом требуется просмотреть массив только в одном направлении – вправо от найденного элемента.
Дадим верхнюю оценку трудоёмкости алгоритма двоичного поиска. На каждой итерации поиска необходимо два сравнение для первой версии, одно сравнение для второй версии. Количество итераций не больше, чем 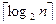 . Таким образом, трудоёмкость двоичного поиска в обоих случаях
. Таким образом, трудоёмкость двоичного поиска в обоих случаях
С=O(log n), n → ∞.
7.2 Варианты заданий
1. Написать программу (язык программирования Паскаль или Си) для быстрого поиска в упорядоченном массиве.
2. Сравнить средние трудоемкости различных версий быстрого поиска.
3. Построить графики зависимости средней трудоемкости поиска от количества элементов в массиве для различных вариантов поиска.
4. Сравнить трудоемкость быстрого поиска с трудоемкостью поиска перебором.
5. Экспериментально оценить долю случаев, когда поиск перебором происходит быстрее, чем быстрый поиск.
8. Сортировка данных с произвольной структурой
8.1 Сравнение данных произвольной структуры
Основная проблема, возникающая при сортировке данных произвольной структуры ¾ неопределенность операции сравнения. Если исходный массив А заполнен числами, то в качестве операции сравнения могут быть использованы стандартные операции сравнения. Если структура сортируемых данных не соответствует простым встроенным типам языка, то необходимо переопределить операции сравнения с помощью логических функций. Например, пусть массив А ¾ телефонный справочник, каждый элемент которого является записью с полями Name (фамилия абонента) и Phone (номер телефона):
 A: Иванов Петров …. Егоров
A: Иванов Петров …. Егоров
223455 452185 454455
Рисунок 26 Список абонентов
Если необходимо отсортировать телефонный справочник по фамилиям абонентов, то логическая функция Less (меньше) может выглядеть следующим образом:
function less ( x,y: <тип записи>): boolean;
begin
less:=x.Name <y.Name;
end;
Такой подход позволяет путем изменения функции Less учитывать любые сложные условия упорядочивания массива элементов произвольной структуры. Например, если необходимо упорядочить телефонный справочник по номерам телефонов дополнительно по фамилиям абонентов, то функцию Less можно записать так:
function less ( x,y: <тип записи>): boolean;
begin
IF (x.phone<y.phone)
less:=true
ELSEIF (x.phone>y.phone )
less:=false
ELSE less:=(x.name<y.name)
FI
FI
end;
Кроме того, нужно переопределить операцию сравнения и при организации поиска элементов в отсортированном массиве. Изменение направления упорядочивания массива достигается путем замены операций сравнения на противоположные, т. е. в самой функции меняем «<» на «>».Операция пересылки не требует переопределения и выполняется путем побитового копирования.
8.2 Сортировка по множеству ключей. Индексация
Пусть рассмотренный выше телефонный справочник необходимо использовать для быстрого поочередного поиска абонентов или по номеру телефона, или по фамилии абонента. Пересортировка массива то по одному, то по другому ключу требует значительных затрат времени. Для эффективного решения подобной задачи используется прием, называемый индексацией, или созданием индексного массива.
Вначале построения индексный массив В заполняется целыми числами от 1 до n. Затем производится сортировка, но при условии, что в операциях сравнения элементы массива А индексируются через массив В. Перестановки делаются только в массиве В. Тогда при доступе к элементам массива А через индексный массив В А[B[i]] можно работать с массивом А как с упорядоченным по возрастанию (например, производить быстрый поиск элементов), в то время как сами элементы А физически не переставляются.
Пример. Рассмотрим создание индексного массива, который упорядочивает массив целых чисел A=(7,1,6,3,2,8,5).Чтобы упорядочивать массив А по возрастанию, пронумеруем его элементы. Введем новый массив В и запишем в него номера массива А в последовательности, соответствующей условию упорядочиванию (по возрастанию). Получим следующий индексный массив В=(2,5,4,7,3,1,6)