Действие магнитного поля на провод с током. Сила Ампера. Работа перемещения провода с током в постоянном магнитном поле

При помещении провода с током в магнитное поле действующая на носители тока магнитная сила передается проводу. Получим выражение для магнитной силы, действующей на элементарный отрезок провода длиной dl в магнитном поле с индукцией В.

Обозначим заряд одного носителя q₁, концентрацию носителей n , скорость упорядоченного движения носителей u , скорость хаотического движения v. Магнитная сила, действующая на один носитель

, (4.2.1)

ее среднее значение равно

.

Здесь , так как все направления скорости хаотического движения равновероятны.

Пусть площадь сечения провода S , тогда объем отрезка провода равен Sdl и общее число носителей nSdl. Суммарная магнитная сила, действующая на элементарный отрезок провода, равна

.

Здесь 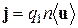плотность тока.

Величина плотности тока j связана с силой тока I и площадью сечения S: j=I/S . Введем вектор элемента длины проводника dl , сонаправленный с вектором плотности тока j, тогда jSdl=Idl и для магнитной силы, действующей на элемент тока, получаем

. (4.2.2)

Это соотношение было получено экспериментально Ампером и называется законом Ампера. Исторически оно было получено раньше, чем выражение для магнитной части силы Лоренца. В действительности, Лоренц получил выражение для магнитной силы, основываясь на законе Ампера.

Для прямого отрезка провода с током I, помещенного в однородное магнитное поле B, сила Ампера равна

. (4.2.3)

Здесь вектор l направлен по току (в сторону переноса положительного заряда), а его модуль равен длине провода. Направление амперовой силы определяется так же, как направление магнитной силы для положительного заряда (см. рис. 4.2.3).

Элементарная работа dА, совершаемая силой Ампера dF_А при перемещении на dr в магнитном поле элемента проводника dl, равна

. (4.2.4)

Здесь мы, подставив выражение для амперовой силы (4.2.2), вынесли скалярную величину – силу тока I и воспользовались известным свойством смешанного произведения векторов: оно не изменяется при циклической перестановке сомножителей. Векторное произведение перемещения и элемента проводника есть вектор площадки, прочерченной проводником при его перемещении (см. рис. 4.2.4):

. (4.2.5)

Скалярное произведение вектора площадки и вектора магнитной индукции – это магнитный поток через площадку dS

, (4.2.6)

поэтому для работы получаем

. (4.2.7)

Если проводник, сила тока I в котором поддерживается постоянной, совершает конечное перемещение из положения 1 в положение 2, то работа амперовых сил при таком перемещении

, (4.2.8)

где Ф_м – магнитный поток через поверхность, прочерченную проводником при рассматриваемом перемещении.

Если в постоянном магнитном поле перемещается замкнутый контур, то поток, прочерченный всеми элементами контура, равен изменению потока пронизывающего контур (так называемого потокосцепления Y). Докажем это.

На рисунке 4.2.5 изображены два последовательных состояния контура С₁ и С₂. Поверхности S₁ и S₂, которые ограничивает контур в положениях С₁ и С₂ и поверхность S_п, прочерченная контуром, составляют замкнутую поверхность. По теореме Остроградского-Гаусса для магнитной индукции суммарный поток через эту замкнутую поверхность равен нулю. Выберем нормали n₁ и n₂ к поверхностям S₁ и S₂ при вычислении потокосцеплений Y₁ и Y₂ в каждом из положений так, чтобы они были согласованы с направлением тока в контуре по правилу правого винта (из конца вектора нормали ток в контуре виден идущим против часовой стрелки). При этом поток наружу из замкнутой поверхности складывается из потока через S₁ в направлении n₁ (равен Y₁), потока через S₂ в направлении противоположном n₂ (равен -Y₂) и потока через прочерченную поверхность S_п (Ф_м). Таким образом, получаем

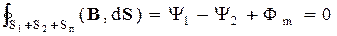, (4.2.9)

откуда . Следовательно, соотношение (4.2.8) для замкнутого контура можно записать так

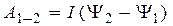. (4.2.10)

При выводе этой формулы мы рассмотрели простое перемещение контура, но она оказывается справедливой и при более сложных изменениях состояния контура, например, при вращении и при деформации. В приведенном виде она выполняется для движении не только одиночного контура, но и катушки, состоящей из нескольких витков, в частности, для катушки из N одинаковых витков. В последнем случае потокосцепление равно Y = NF_м, где F_м – магнитный поток через один виток.

36) Магнитный диполь. Магнитный момент тела и его намагниченность.

(adsbygoogle = window.adsbygoogle || []).push({});

 

В каждом атоме электроны движутся вокруг центрального ядра, т.е. возникает элементарный электрический ток.

Векторная величина, равная произведению тока i и элементарной площади S, ограниченной элементарным контуром с током, и направленная перпендикулярно к этой площадке согласно правилу Буравчика, называется магнитным моментом элементарного электрического тока.

 

Геометрическая сумма магнитных моментов всех элементарных электрических токов в теле, дает магнитный момент тела М,

т.е. М=m₁+m₂+m₃+…

величина, измеряемая отношением магнитного момента тела к его объему (V), называется намагниченностью тела Y.

37) Алгоритм расчета неразветвленной магнитной цепи. Магнитодвижущая сила (МДС).

Электромагниты широко применя­ются в таких электрических аппаратах, как контакторы, пускатели, реле, автоматы, электромагнитные муфты и т. д.

Основные соотношения для магнитной цепи элек­тромагнита рассмотрим на примере клапанной си­стемы (рис. 4.4). Подвижная часть магнитной цепи, соз­дающая рабочее усилие, называется якорем 1. Участки магнитопровода 3 и 4 называют стержнями или сер­дечниками.

В клапанной системе якорь может иметь как поступа­тельное, так и вращательное движение.

При прохождении тока по намагничивающей катушке 2 создается МДС, под действием которой возбуждается магнитный поток Ф. Этот поток замыкается как через за­зор 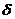, так и между другими частями магнитной цепи, име­ющими различные магнитные потенциалы.

Воздушный зазор 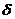, меняющийся при перемещении якоря, называется рабочим. Соответственно магнитный поток, проходящий через рабочий зазор, называется рабочим магнитным потокоми обозначается . Все остальные потоки в магнитной цепи, не прохо­дящие через рабочий зазор, назы­ваются потоками рассеяния .Электромагнитное усилие, раз­виваемое якорем, определяется маг­нитным потоком в рабочем зазоре .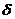

При расчете магнитной цепи оп­ределяется МДС катушки, необхо­димая для создания заданного ра­бочего потока (прямая задача), ли­бо рабочий поток по известной МДС катушки (обратная задача). Эти за­дачи могут быть решены с помощью законов

Кирхгофа для магнитной цепи. Согласно первому закону Кирх­гофа, алгебраическая сумма потоков в любом узле магнитной цепи равна нулю

.

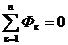(4.1)

Второй закон Кирхгофа следует из известного закона полного тока

,

(4.2)

где Н - напряженность магнитного поля; 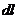- элементар­ный участок контура интегрирования; - алгебраи­ческая сумма МДС, действующихв контуре.

Так как , то формулу (4.2) можно записать так:

, или , (4.3)

где 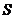- сечение данного участка магнитной цепи; 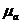- абсолютная магнитная проницаемость участка 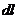, равная ; здесь - магнитная постоянная, -относительная магнитная проницаемость.

Магнитная проницаемость 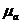характеризует магнитную проводимость материала цепи.

Для воздуха магнитная проницаемость берется равной магнитной постоянной .

Выражение аналогично выражению для актив­ного сопротивления элемента электрической цепи (где - удельная электрическая проводимость материа­ла проводника). Тогда формулу (4.3) можно представить в виде 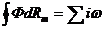, (4.4)

где - магнитное сопротивление участка длиной .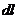

Падение магнитного потенциала по замкнутому конту­ру равно сумме МДС, действующих в этом контуре. Это и есть второй закон Кирхгофа для магнитной цепи.

Когда поток в отдельных участках магнитной цепи не меняется, интеграл в (4.4) можно заменить конечной сум­мой

. (4.5)

Таким образом, сумма падений магнитного напряжения по замкнутому контуру равна сумме МДС, действующих в этом контуре.

Направление МДС, совпадающее с направлением об­хода контура, принимается за положительное, противопо­ложное ему - за отрицательное. За направление обхода обычно принимается направление магнитного потока. Из формулы (4.5) вытекает закон Ома для магнитной цепи, при этом вместо тока подставляется магнитный поток, вместо элек­трического сопротивления - магнитное и вместо ЭДС под­ставляется МДС.

По аналогии с электрическим, магнитное сопротивление участка конечной дли-ны I можно представить как ,

где - магнитное сопротивление единицы длины магнит­ной цепи при сечении, также равном единице, м/Гн.

Для расчета по формуле (4.5) необходимо знать . Если зада­на не кривая 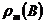, а кривая намагничивания материала 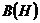, для расчета удобно использовать формулу (4.2). Если на отдельных участках индукция постоянна, то интеграл в (4.2) можно заменить конечной суммой

(4.6)

По известной индукции в каждом участке с помощью кривой 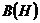находят напряженность , после чего с по­мощью равенства (4.6) можно

отыскать МДС катушки.

При расчете магнитной цепи часто более удобна вели­чина, обратная магнитному сопротивлению, – магнит­ная проводимость, Гн.

.

Уравнение (4.5)

при этом принимает вид .

Для простейшей неразветвленной цепи с проводимо­стью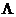

, или

.

(4.7)

Магнитное сопротивление и проводимость ферромаг­нитных материалов являются сложной нелинейной функ­цией индукции. Нелинейная зависиles/image117.gif" /> - длина зазора.

Данным выражением можно пользоваться при соотношени­ях > 20, где а и - размеры прямоугольных полюсов; - диаметр круглого полюса.

При больших рабочих зазорах у краев полюсов возни­кает дополнительный поток, называемый потоком вы­пучивания. В результате при данном значении разно­сти магнитных потенциалов полный поток из полюса уве­личивается. Магнитная проводимость, равная отношению потока к разности магнитных потенциалов, возрастает по сравнению с , не учитывающей поток выпучи­вания.

Расчет проводимости с учетом выпучивания связан с большими трудностями, ввиду сложности картины магнитного поля. Для расчета используются три основных метода:

1) Расчет по эмпирическим формулам. Так, например, для проводимости между торцами цилиндрических полюсов диа­метром достаточно точный результат дает формула

.

Последних два слагаемых учитывают поток выпучивания. Для прямоугольных полюсов с поперечными размерами а и достаточ­но точна формула

.

2) Когда аналитический расчет проводимости затруднен вследствие сложной картины поля, реальное поле разбивается на простые геометрические фигуры, для которых существуют расчетные формулы определения проводимостей. Результирующая проводимость определяется по сумме проводимостей отдельных фигур.

3) Если проводимость не может быть рассчитана первыми двумя методами, необходимо графически построить картину магнитного поля. Поле разбивается на элементарные трубки, в пределах которых поток одинаков, и определяется проводимость трубки. Полная проводимость определяется суммарной проводимостью всех трубок.

38) Явление переменного тока. Получение синусоидальной ЭДС

 

За один оборот рамка развернется на угол , а время оборота – период (Т), тогда угловая частота определяется: