Функция распределения непрерывной случайной величины
Пусть Х – непрерывная случайная величина и 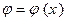 - ее плотность распределения. Используя определения функции распределения (см. § 3.4) и плотности распределения, получаем
- ее плотность распределения. Используя определения функции распределения (см. § 3.4) и плотности распределения, получаем
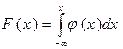 .
.
Обратно, если задана функция распределения непрерывной случайной величины, то (см. теорему об интеграле с переменным верхним пределом) плотность распределения этой случайной величины будет определяться равенством
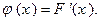
Таким образом, имеется два равноправных способа задания непрерывной случайной величины: с помощью или плотности распределения, или функции распределения.
Пример.Пусть плотность распределения непрерывной случайной величины Х имеет вид:
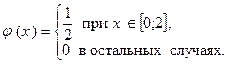
Найти функцию распределения.
Решение.Пусть 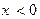 . Тогда
. Тогда
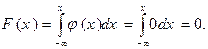
Если 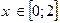 , то
, то
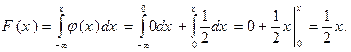
Если 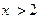 , то
, то
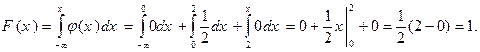
Таким образом, окончательно, искомая функция распределения имеет вид
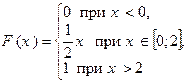
(см. рис. 6).