Метод золотого сечения.

Метод основан на делении текущего отрезка [а, b], где содержится искомый экстремум, на две неравные части, подчиняющиеся правилу золотого сечения, для определения следующего отрезка, содержащего максимум.

Золотое сечение определяется по правилу: отношение отрезка к большей его части равно отношению большей части отрезка к меньшей. Ему удовлетворяют две точки с и d, расположенные симметрично относительно середины отрезка.

 

Рис. 3.3. Иллюстрация метода золотого сечения:

1 — интер­вал, включающий в себя иско­мый максимум функции после

первого этапа (первого золото­го сечения в точках c и d);

2 — то же, после второго этапа (но­вая точка еи старая точка d

 

Путем сравнения R(с)и R(e)определяют следующий отрезок, где содержится максимум. Если R(e) > R(с), то в качестве сле­дующего отрезка выбирается отрезок [с, b], в противном слу­чае — отрезок [a, e].

Поэтому на каждой следующей итерации (кроме "запуска" метода на исходном отрезке) нужно вычислять только одно зна­чение критерия оптимальности.

Новый отрезок снова делится на неравные части по правилу золотого сечения. Следует отметить, что точка d является и точ­кой золотого сечения отрезка [с, b], т.е.

Обозначим коэффициент золотого сечения k=db/cd, тогда можно получить квадратное уравнение для его нахождения

 

k=0,618

 

Решение уравнения применительно к первой итерации имеет вид

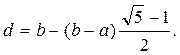
Условие окончания поис­ка — величина отрезка, содер­жащего максимум, меньше за­данной погрешности.

Метод обеспечивает более быструю сходимость к реше­нию, чем многие другие ме­тоды, и применим, очевидно, только для одноэкстремальных функций.

Пример.

Дана функция

R(x)=sin(x+1),

Найти макси­мум на интервале: [-1,2]. Ошибка задается по х: e =0,05.

Результаты расчетов. Для "запуска" метода найдем две симметричные точки золотого сечения для отрезка [-1, 2]:

х₁ = 0,145898, х₂ = 0,85410197.

Значения критериев в этих точках соответственно R(x₁) = 0,911080, R(x₂)= 0,960136. Следовательно, новым отрезком является [0,145898,2], внутри которого находится максимальное из найденных значений R. Точка золотого сечения для нового отрезка будет х₃= 0,58359214, a R(x₃) = 0,99991813.

Далее приведены только координаты лучших точек при очередном шаге, номер шага и значения критерия в этих точках.

x₃ = 0,584 R₃ = 0,9999 x₄ = 0,584 R₄ = 0,9999

 

С точностью до четырёх значащих цифр задача решена на третьей итерации

d)

Рис. 3.4