ОБРАТНАЯ МАТРИЦА

Пусть А – квадратная матрица. Обратной к ней называется такая матрица А^–1, что 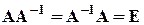(единичная).

По свойству 6 определителей 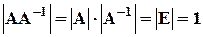, поэтому 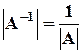. Значит, если|A| =0, то для такой матрицы обратной найти невозможно. Матрицы А, у которых |A| =0, называются вырожденными. Если же 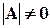, то матрица называется невырожденной.

Научимся находить обратную для невырожденной матрицы. Для этого построим матрицу А^*, составленную из алгебраических дополнений:

.

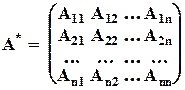Здесь А_ij – алгебраическое дополнение к элементу a_ij, т.е. минор с учётом знака.

Теорема 2. Если А – невырожденная квадратная матрица, 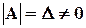, то для

неё существует обратная матрица, которую можно найти по формуле:

.

Для невырожденной матрицы Аимеется только одна обратная матрица А^–1 – та, которую мы построили. Действительно, если Вкакая–либо другая матрица со свойством: АВ=Е,то В=(А^–1А)В=А^–1(АВ)=А^–1Е=А^–1,т.е. В=А^–1.