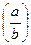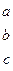Количественный подход к анализу поведения потребителей. Полезность. Первый закон Госсена.

1. Запустите редактор формул, для этого выполните команду: Вставка-Объект

2. Выберите тип объекта: функция(формула).

3. В команде Вид должна быть включена опция Выбор.

4. Открываются:

а) окно Выбор с командами;

б) в нижней части экрана окно редактирования формул с мигающим курсором;

в) в исходном тексте обозначено место ввода формулы.

5. Рассмотрим команды окна Выбор (их 9) {нажатие клавиши соответствующей команды делает ее активной}

+a a-b

унарные (бинарные) операторы.

Нажав эту клавишу, получаем возможность набирать следующие операции: +a, -a, ±a, >a, a+b, a_*b, … , a÷b, a/b, … (посмотреть их все на лабораторной работе).

{<?>}

< ? >

Пример:

курсор

Наши действия: Y= = over

В текстовом документе: Y = x – 2 over 4

В текстовом документе: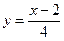

a≤b

2) - отношения {a = b, a ≠ b, a ≈ b, a│b …}

Пример: y =(a + b) ≥ π

a≤b

a≥b

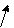Наши действия: Y = y = <?> ≥ <b>

newline (a+b)

«новая строка» ∑ - Символы выбираем π – вставить

Строка редактора формул:

Y = (a+b) geslant % ρi

Строка текстового документа Y = (a+b) ≥ π

Зам: если мы хотим набирать сл.ф.: нужно набрать команду Newline y =

3) a 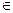A – операции над множествами

{ACB, A , … }// посмотреть на лаб.работе

4) f(x) – функции { }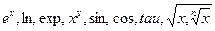

Пример: y =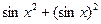

Наши действия:

Y = <?> + <?>

f(x)

x^y

sin (<?>) <?> ^ {<?>}

x^y

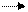
sin

<?> ^ {<?>} sin(<?>)

x 2 x

т.д.: y = sin(x²) + sin(x)²

∑a

5) - операторы {

}

Пример: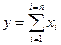

Наши действия:

∑a

∑x

Y= Sum <?>

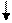
from{ <?>}to{<?>}<?>

i=1 i=n

x_b

<?> {<?>}

x _ i

6) Атрибуты { } посмотреть на л.р.

B – жирный шрифт,

I – наклонный шрифт.

7) -прочее { } – на лаб.работе.

Пример: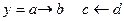

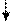Наши действия: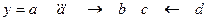

Пробел (~)

8) скобки { }-посмотреть на лаб.р.

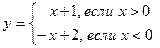
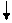
Наши действия: Y= left lbrace <?> right rbrace

none

binom { <?>} { <?>}

x + 1 -x + 2

Т.д.:

Редактирование: Выравнивание - из A выбрать (пробел) и вставить, где нужно.

9) Форматы (Шаблоны ) { , ,

см.в л.р.}

Пример:

переход на новую строку

matrix{<?>#<?># #<?>#<?>}

x_b

<?> -{11}

matrix {<эл> # <эл> # #<эл> # <эл>}

1строка 2 строка

Количественный подход к анализу поведения потребителей. Полезность. Первый закон Госсена.

В современной микроэкономике упрощенно полагают, что поведение потребителя полностью определяется его стремлением максимизировать некоторый показатель, называемый по-разному: удовольствие, наслаждение, удовлетворение, желаемость, ценность, польза и т.д. Мы будем следовать традиции, и использовать термин полезность.

Существует два подхода к анализу поведения потребителя: количественный и порядковый.

1. Количественный (кардиналистский) подход.Основан на предположении о возможности измерения полезности различных благ в гипотетических единицах ютилях (от англ. utility – полезность). Такие оценки имеют индивидуальный, субъективный характер: один и тот же продукт может представлять большую ценность для одного потребителя и не представлять – для другого. Поэтому этот подход не предусматривает возможности сравнения.

Важнейшим понятием кардиналистской теории потребителя является функция полезности. Это зависимость полученной человеком полезности от объемов потребления продуктов. При моделировании поведения с помощью этой функции кардиналисты делают ряд упрощений.

«Ютили» разных потребителей несравнимы и поэтому не могут суммироваться. Полезность может быть как положительной (наслаждение) так и отрицательной (страдание). Если количество потребленного продукта выражается целым числом, то такой продукт называют неделимым (конфеты, вишни). Если количество продукта может выражаться любым дробным числом, то этот продукт называют делимым (молоко, соль). Потребляемые продукты в той или иной степени способны замещать друг друга при сохранении величины полезности. Цель потребителя состоит в максимизации полезности при данных затратах.

Кардиналисты рассматривают предельную полезность продукта – это прирост полезности набора продуктов при увеличении объема потребления данного продукта на единицу. Она зависит как от функции полезности, так и от исходного набора продуктов, к которому добавлена еще одна (последняя, маргинальная) единица. Предельная полезность обозначается MU (от англ. marginal – предельный, последний). Полезность же называют общей полезностью и обозначают TU.

Если продукт неделим, то предельная полезность i-й ед. продукта равна изменению полезности (разности полезности до и после ее потребления):

MU_i = U_i – U_i_-1.

Если продукт делим, то предельная полезность х единиц продукта равна приросту общей полезности, приходящемуся на бесконечно малый прирост потребления сверх объема х. Т.е. в данном случае предельная полезность равна производной функции общей полезности:

MU(x) = ΔU/Δx = U'(x)

Основное свойство предельной полезности выражается первым законом Госсена,или законом насыщения потребностей. Согласно ему с ростом потребления одного продукта (при неизменном объеме потребления всех остальных) предельная полезность убывает, т.е. общая полезность возрастает все более низкими темпами, а убывает – все более высокими.