Масштаб длин, масштабы по меридианам и параллелям

Масштаб длин из формулы (2)

Но

Рис. 2.1. Элементарный сфероидический треугольник

Из элементарного сферического треугольника (рис. 2.1).

В этом треугольнике бесконечно малая дуга меридиана

Где радиус кривизны меридиана.

Из сфероидической геодезии известно, что радиус кривизны меридиана

Где большая полуось эллипсоида вращения, его эксцентриситет.

Бесконечно малая дуга параллели

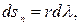
Где радиус кривизны параллели радиус кривизны первого вертикала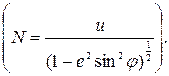

Тогда можем написать

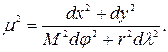
На основании формулы (1) полные дифференциалы равны:

Отсюда

(4)

В этой формуле использованы следующие известные коэффициенты Гаусса:

Подставим (4) в формулу масштаба и получим

После введения вспомогательной функции (путем деления числителя и знаменателя на ) получим

(5)

Найдем значение из элементарного сферического треугольника (рис. 2.1)

(6)

И подставим в (5)

Введем обозначения

(7)

Где эксцентриситет эллипсоида, радиус кривизны меридиана, точка на меридиане эллипсоида, функции проекции, радиус кривизны параллели, средний радиус кривизны эллипсоида.