И статистическая обработка результатов анализа

 

Значение измеряемого аналитического сигнала – случайная величина. Для характеристики результата анализа применяют понятия «правильность», «точность», «воспроизводимость», «чувствительность».

Мерой точности и воспроизводимости является величина случайной ошибки. Для некоторой концентрации С_i абсолютная случайная ошибка

Δ_сл = │С_i – Ĉ│;

относительная случайная ошибка

δ_сл =│(С_i – Ĉ)│ / Ĉ,

где Ĉ – среднее арифметическое значение нескольких определений.

Мерой правильности является величина систематической ошибки. Для некоторой концентрации С_i абсолютная систематическая ошибка

Δ_сист = │С_ист – Ĉ│;

относительная систематическая ошибка

δ_сист = │(С_ист – Ĉ)│/ С_ист,

где С_ист – истинное значение определяемой концентрации.

Систематические ошибки (например, смещение шкалы при настройке измерительного прибора) устранимы. Случайные ошибки полностью устранить нельзя, их можно только уменьшить. Случайные ошибки делают неточным результат анализа, а систематические –неверным сам анализ.

Чувствительность метода оценивают по крутизне зависимости в координатах «аналитический сигнал – концентрация определяемого вещества». Первую производную аналитического сигнала А по концентрации называют коэффициентом чувствительности k (или чувствительностью):

.

Например, при фотометрическом определении Fe³⁺ используют его поглощающие свет комплексы с тиоцианат-ионами SCN^– или анионами сульфосалициловой кислоты C₆H₃(OH)(COOH)SO₃^–. Из рис. 1. следует dА₂/d(C) > dА₁/d(C). Таким образом, второй метод чувствительнее первого.

Рис. 1. Зависимость оптической плотности раствора от концентрации Fe³⁺

для тиоцианатных (1) и сульфосалицилатных (2) комплексов

 

В фотометрии аналитический сигнал «оптическая плотность» А связан с толщиной слоя раствора l и концентрацией законом Бугера:

А = ε · l · C

В уравнении закона Бугера молярный коэффициент поглощения εявляется мерой чувствительности (коэффициентом чувствительности).

Обычно наблюдаемые в аналитической практике случайные значения подчиняется закону нормального распределения Гаусса (рис. 2):

,

где y – плотность вероятности распределения случайной величины х_i; μ– математическое ожидание (среднее арифметическое значение для генеральной совокупности); σ – среднее квадратичное отклонение (расстояние от μ до проекции точки перегиба на ось х).

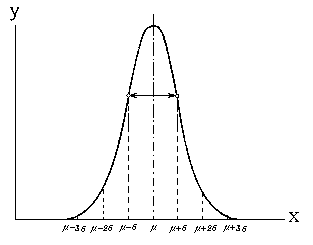
Рис. 2. Кривая Гаусса

При проведении серии из n параллельных измерений в качестве результата выбирают среднее значение и приводят метрологические характеристики результатов анализа. Важнейшей из них является доверительный интервал ε:

где t_α,f – значение критерия Стьюдента для доверительной вероятности α и числа степеней свободы f; σ – среднее квадратичное отклонение.

Расчет величины σ ведут по формуле

.

Подробное описание этапов статистической обработки результатов анализа дано в приложении 2.