Обработка результатов измерений.

Цель работы.

Исследовать резонансные явления в параллельном контуре на физической модели и резонансные явления в последовательном контуре на электронной модели в пакете Workbench.

Исходные данные.

Вариант 1.

Схема цепи.

Рис. 1. Схема цепи последовательного контура.

Результаты измерений.

Таблица 1.

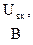
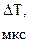
		29,53	30,31	9,960	463,5		5,30	3,9
		29,63	30,27	9,980	464,0		5,09	3,7
		29,73	30,23	9,980	464,3		2,00	1,5
		29,82	30,17	9,990	464,6		2,70
		29,91	30,11	9,990	464,8		1,50
		29,99	30,04	9,990	464,8		0,00
		30,05	29,96	10,000	464,9		-2,00	-1,5
		30,13	29,89	9,990	464,7		-3,00	-2,2
		29,41	30,34	9,950	463,0		7,60	5,6
		29,30	30,37	9,940	462,3		10,10	7,5
		29,19	30,40	9,922	461,5		10,10	7,5
		29,06	30,42	9,903	460,6		10,00	7,4
		28,93	30,43	9,883	459,7		11,20	8,4
		28,80	30,43	9,862	458,7		12,50	9,4

 

Обработка результатов измерений.

По экспериментальным данным построим графики (в одних осях) следующих зависимостей: .

Рис. 2. Графики экспериментальных зависимостей.

 

Построим графики тех же зависимостей, но полученных путем расчетов в пакете MathCAD. Для этого начертим расчетную схему:

Рис. 3. Расчетная схема.

Запишем второй закон Кирхгофа:

,

откуда найдем зависимость тока от частоты:

.

Найдем также выражения и для напряжений и разности фаз:

;

;

;

.

Зададим в пакете MathCAD параметры схемы:

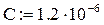
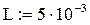
Определим комплексный ток как функцию от частоты, а также найдем его действующее значение:

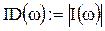
Определим комплексное напряжение на конденсаторе и его действующее значение:

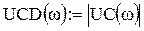
Определим комплексное напряжение на катушке и его действующее значение:

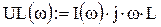
Определим комплексное напряжение на резисторе и его действующее значение:

Определим фазовый сдвиг между током и напряжением источника:

Зададим последовательность изменения частоты:

Для лучшего отображения графиков всех зависимостей в одних осях, ток увеличим в 10 раз, а графики напряжений опустим по оси ординат так, чтобы они оказались близко к графикам остальных зависимостей:

Построим график всех зависимостей в одних осях:

Рис. 4. Графики теоретических зависимостей.

По результатам измерений (табл. 1) построим векторные диаграммы токов и напряжений в резонансном режиме и при отклонении от этого режима в одну и другую стороны.

1. Режим резонанса.

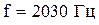
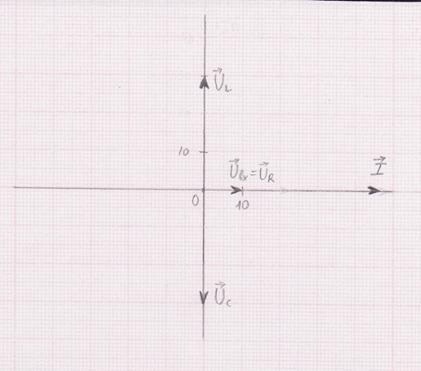
Рис. 5. Векторная диаграмма токов

и напряжений при резонансе.

2. Отклонение от резонанса в сторону меньшей частоты.

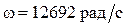
Рис. 6. Векторная диаграмма токов и напряжений

при отклонении от режима резонанса.

 

3. Отклонение от резонанса в сторону большей частоты.

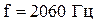
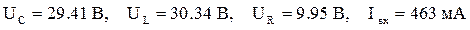
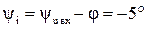
Рис. 7. Векторная диаграмма токов и напряжений

при отклонении от режима резонанса.

 

Вывод.

В ходе работы был исследован последовательный контур и установлено, что в режиме резонанса разность фаз между током и напряжением источника равна нулю, ток максимален, действующие значения напряжений на индуктивных и емкостных элементах равны между собой и в несколько раз превышают входное напряжение.