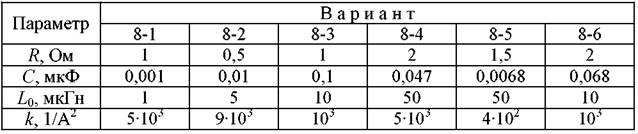
Содержание отчета
Лабораторная работа №3
Модели колебательных систем
Порядок выполнения работы
1. Формализуйте задачу для решения на ЭВМ.
2. Выберите программную реализацию решения (с помощью специальных процедур в MATLAB или в виде отдельной программы).
3. Выполните расчет на ЭВМ, используя разные шаги интегрирования.
4. Оформите отчет по работе.
Содержание отчета
1. Цель работы.
2. Задание.
3. Описание метода решения – сведения из теории (формулы, алгоритм).
4. Распечатка решения задачи на ЭВМ, включая графики и комментарии.
5. Краткие выводы по работе
 |
Ниже приведены варианты заданий. Каждое из заданий включает ряд вариантов, отличающихся друг от друга набором исходных данных.
Задание 1. Для защиты от вибрации приборный блок установлен специальные на упругие опоры (амортизаторы). Его движение на амортизаторах при отсутствии боковых и крутильных колебаний описывается дифференциальным уравнением вида

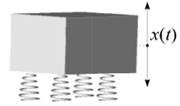
где x – отклонение блока от исходного положения, t – время, m – масса блока, d2x/dt2 – ускорение, β – коэффициент трения (в амортизаторах), dx/dt – скорость движения при колебаниях блока, kx – слагаемое, отвечающее за сопротивление упругих элементов (пружин), k – коэффициент жесткости амортизаторов. Суммарная жесткость пружин зависит от деформации x: k = k0 (1 + ax2).
Решите уравнение при следующих данных: β = 0,5 кг/с;
начальные условия x = 1 см, dx/dt = 0 при t = 0.
Остальные параметры заданы в таблице.
Получите точки решения, охватывающие не менее пяти периодов колебаний, и постройте по ним соответствующий участок зависимости x(t).

Задание 2. Приборный блок установлен на упругие опоры (амортизаторы). Его вертикальные колебания описывается дифференциальным уравнением, приведенным в задании 1.
Амортизаторы имеют встроенные демпфирующие элементы. Поэтому коэффициент трения β в системе зависит от деформации x: β = β0 (1 + ax2).
Решите уравнение для следующих исходных данных: коэффициент трения k = 1 Н/м; начальные условия x = 1,5 см и dx/dt = 0 при t = 0. Остальные параметры заданы в таблице.
Получите начальные точки решения, охватывающие несколько периодов колебаний, и постройте по ним соответствующий участок зависимости x(t). 
 Задание 3. Вертикальные колебания механической системы (см. задание 1) под действием вынуждающей силы описывается уравнением вида
Задание 3. Вертикальные колебания механической системы (см. задание 1) под действием вынуждающей силы описывается уравнением вида

где x – отклонение системы от исходного положения, t – время, m – масса блока, β – коэффициент трения, k – коэффициент жесткости амортизаторов.
Внешнее воздействие представляет собой периодическую последовательность ударных импульсов F(t)
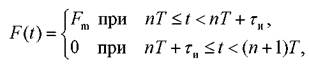
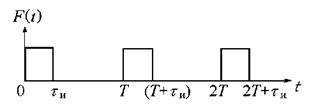
Где n = 0, 1, 2, 3, 4… .
Решите уравнение для следующих данных: масса m = 1 кг; коэффициент трения β = 0,5 кг/с, коэффициент жесткости k = 5 Н/м.
Начальные условия x = 0 и dx/dt = 0 при t = 0.
Остальные параметры даны в таблице.
Получите начальные точки решения, охватывающие не менее трех периодов колебаний. Постройте зависимости F(t) и x(t).

Задание 4. Вертикальные колебания механической системы (см. задание 1) под действием последовательности полусинусоидальных импульсов описывается дифференциальным уравнением вида
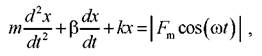
где x – отклонение системы от исходного положения, t – время, m – масса блока, β – коэффициент трения, k – коэффициент жесткости амортизаторов, Fm и ω – параметры вынуждающей силы.
Решите уравнение для следующих данных: масса m = 3 кг; коэффициент трения β = 1 кг/с, коэффициент жесткости k = 4 Н/м. Начальные условия x = 0 и dx/dt = 0 при t = 0. Остальные параметры даны в таблице.
Получите участок решения x(t), на котором устанавливаются устойчивые колебания в системе. Постройте зависимости F(t)=|Fmcos(ωt)| и x(t).

Задание 5. Прогиб однородной балки под собственным весом при консольном закреплении описывается дифференциальным уравнением


где L - длина балки, Р - удельный вес балки (на единицу длины), EJ - жесткость балки, х - координата (0 < х < 1). Задавшись начальными условиями
у = 0 и у' = 0 при х = 0, получите точки решения на всей длине балки для указанных параметров.

Задание 6. Количество особей в популяциях двух видов, взаимодействующих между собой по типу жертва - хищник, равно соответственно х и у. Изменение популяций во времени описывается системой дифференциальных уравнений (модель Лотки-Вольтерра)

где t - время, ах - скорость размножения жертв, bху - скорость их истребления с учетом частоты встреч с хищниками, су - скорость вымирания хищников, dxy - скорость размножения хищников в присутствии жертв.
Задавшись параметрами а, b, с, d и приняв начальные условия x0, у0 при t=0, решите задачу. Получите участок решения, на котором наблюдаются повторяющиеся колебания численности популяций. Постройте соответствующие графики x(t), y(t) и у(х).

Задание 7. Развитие популяций хищников и их жертв описывается моделью Холлинга-Тэннера:
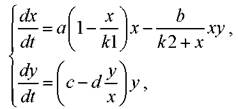
где х и у - относительная численность жертв и хищников соответственно, t - время, ах - скорость размножения жертв, ах2/k1 - учитывает конкуренцию жертв из-за пищи, bху/(k2+х) - скорость истребления жертв хищниками с учетом насыщения последних, су - скорость размножения хищников, cdy2/x - учитывает вымирание хищников при недостатке пищи х.
Используя заданные в таблице параметры и начальные условия x0, у0 получите участок решения, описывающий колебания x(t) и y(t).

Задание 8. Свободные колебания тока в последовательном электрическом колебательном контуре описываются дифференциальным уравнением
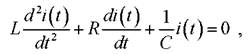
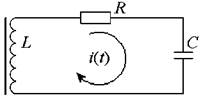
где i - ток, L - индуктивность катушки, R - сопротивление потерь контура, С - емкость конденсатора. Предполагается, индуктивность катушки зависти от протекающего через нее тока: L =L0 (1 - ki ), где k - коэффициент.
Рассчитайте и постройте график зависимости i(t), охватывающий не менее пяти периодов колебаний, для начальных условий di/dt = 0 и i=10 мА при t = 0. Остальные параметры указаны в таблице.