ВСЕ ЛЕКЦИИ ПО ТЕОРИИ МЕНЕДЖМЕНТА

Рассмотрим вкратце некоторые смежные понятия. Поток событий называется потоком Пальма (или потоком с ограниченным последействием), если промежутки времени между последовательными событиями:

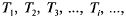
представляют собой независимые, одинаково распределенные случайные величины.

Простейший поток есть частный случай потока Пальма: в нем расстояния 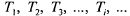представляют собой случайные величины, распределенные по одному и тому же показательному закону; их независимость следует из того, что простейший поток есть поток без последействия, и расстояние по времени между любыми двумя событиями не зависит от того, каковы расстояния между другими.

Многие потоки событий, встречающиеся на практике, хотя и не являются в точности потоками Пальма, но могут быть ими приближенно заменены.

Важными для практики образцами потоков Пальма являются так называемые потоки Эрланга. Эти потоки образуются в результате «просеивания» простейших потоков.

Например, если из точек на оси t (рис. 5.3) сохранить не все точки, а только каждую вторую, то в результате такой операции «просеивания» образуется снова поток событий; он называется потоком Эрланга второго порядка.

Вообще, потоком Эрланга к-то порядка называется поток, получающийся, если в простейшем потоке сохранить каждую k-го точку, а остальные выбросить. Очевидно, простейший поток представляет собой частный случай потока Эрланга, а именно поток Эрланга 1-го порядка

Интервал времени Т между соседними событиями в потоке Эрланга k-го порядка представляет собой сумму к независимых случайных величин - расстояний между событиями в исходном простейшем потоке:

Каждая из этих случайных величин распределена по показательному закону (5.17).

Закон распределения интервала T между соседними событиями в потоке 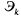называется законом Эрланга k-го порядка.

Нетрудно получить следующие выражения для матожидания, дисперсии и среднего квадратичного отклонения для интервала событий в потоке Эрланга k-го порядка:

 

ВСЕ ЛЕКЦИИ ПО ТЕОРИИ МЕНЕДЖМЕНТА