Ошибки измерений

Во время написания данной работы, я открыл для себя довольно-таки много интересного. Не мог когда-то предположить, что психология и строительство могут быть столь сильно связаны. Я был очень увлечен написанием данной работы. Очень полезной была информация про самоактуализацию, потребности по А. Маслоу, тест К. Томаса на решение конфликтов, а так же типы лидерства.

Крайне полезной считаю информацию про решение конфликтов в коллективе, самоактуализацию и мотивацию, планирую в дальнейшем применять полученные знания в жизни.

 

Список литературы:

1. Большаков А. Г., Несмелова М. Ю. Конфликтология организаций. М., 2001.

2. Вахрешев, А. Политическое лидерство [Текст]/ А. Вахрешев – М: Гелиос, 2003.

3. Кравченко, А. Социология и политология [Текст]/ А. Кравченко.– М.: Дрофа, 2000.–439с. – с.78, 80.

4. Кричевский Р. Л., Дубовская Е. М. Социальная психология малой группы, М.: Изд. Аспект Пресс, 2001.

5. Маслоу А. Мотивация и личность. СПб., 1999.

6. Мухаев, Р. Политология [Текст]/Р. Мухаев.– М.: Пиор – издат, 2003.– 432 с.

7. Панарин, А. Политология [Текст]/ А. Панарин.– М.:ПБОЮЛ С.М. Грачев, 2000.– 448 с. – с.22

8. Рубинштейн С. Основы общей психологии. СПб., 1999.

9. Тутушкина М. Практическая психология, 2001

10. Чередниченко И. П., Тельных Н. В. Психология управления. — Ростов-на-Дону: Феникс, 2004. — 608 с.

 

САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ АРХИТЕКТУРНО-СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ

 

Контрольная работа по курсу:

«Психология и педагогика»

 

 

Выполнил: Каретников Вадим Викторович

Группа: ТГВ-СЗ-4

Шифр: 11-137

Проверил(а):

Санкт-Петербург

2014г.

 

Ошибки измерений

2.1. Виды ошибок измерений и источники их возникновенияИзмерения рассматриваются с двух точек зрения: количественной, выражающей числовое значение измеренной физической величины и качественной , характеризующей точность измерения. Результаты измерений не являются точным значением измеряемой величины, а несколько отличаются (отклоняются) от него. Отклонение измеренной величины ℓ от ее истинного (точного) значения Х называется истиннойошибкой или погрешностью измерения и обозначается D. Ошибки всегда имеют величину и знак плюс или минус. Величина ошибки показывает на сколько измеренное значение отклонилось от истинного; знак - в какую сторону произошло отклонение. Ошибки характеризуют точность измерения, т.е. степень близости измеренной величины к ее истинному значению. Чем меньше ошибка, тем точнее измерение. На результат измерения оказывают влияние многие факторы и каждый из них порождает свою часть общей ошибки. Ошибки, происходящие от отдельных факторов, называют элементарными. Х - ℓ = D или ℓ - Х = D (1) Ошибка (погрешность ) результата измерения является алгебраической суммой элементарных ошибок: [D] = D₁ + D₂ + D₃ + … + D_n (2) Квадратные скобки означают знак суммы ( ввел Гаусс). Ошибки различают по двум признакам: по источнику возникновения (происхождения) и по характеру действия. По источнику возникновения ошибки подразделяют на приборные (инструментальные), методические, личные и внешние. Приборные или инструментальные ошибки обусловлены неточным изготовлением и сборкой отдельных деталей и узлов приборов, неточной установкой их во время измерений и др. причинами. Методические ошибки возникают из-за несоблюдения методики измерений. Личные ошибки связаны с особенностями органов зрения человека выполняющего измерения (наведение зрительной трубы на удаленный предмет, оценку доли наименьшего деления шкалы «на глаз»каждый человек делает по- разному). Внешние ошибки возникают из-за воздействия внешней среды в которой производятся измерения: температура, давление и влажность воздуха; неравномерное нагревание солнцем отдельных частей приборов; степень освещенности; ветер, турбулентность воздуха и др. По характеру действия ошибки разделяют на систематические и случайные. Кроме того, результаты измерений могут содержать грубыеошибки. Грубыми считают ошибки, превосходящие по абсолютной величине некоторый установленный предел. Они появляются главным образом в результате промахов и просчетов из-за невнимательности или недостаточной квалификации (опытности) исполнителя. Их выявляют путем повторных (контрольных) измерений. Измерения, содержащие грубые ошибки, не берут в дальнейшую обработку, бракуют и заменяют новыми. С целью выявления грубых ошибок все геодезические измерения выполняют с контролем, не менее двух раз: углы измеряют при двух положениях теодолита; длины линий - в прямом и обратном направлениях; превышения - по двум сторонам рейки и в прямом и обратном ходах. Систематическими называют ошибки, которые по знаку или величине однообразно повторяются в многократных измерениях какой-либо величины. Для их выявления считают число положительных и отрицательных ошибок и их сумму. При отсутствии систематической части общей ошибки число ошибок с разными знаками примерно одинаковое и суммы их также примерно равны между собой. Они возникают из-за приборных, методических, личных и внешних факторов. Например, несоответствие фактической длины мерного прибора указанному на нем. Систематические ошибки различают по характеру проявления. Они могут быть: а) переменные, прогрессивного типа; б) односторонне действующие; в) периодические; г) постоянные; д) смешанные. Систематические ошибки прогрессивно типа в процессе измерений возрастают или убывают. Такого рода ошибки возникают, например , при измерении линий стальной лентой, длина которой больше или меньше номинальной. Если ряд ошибок с переменными абсолютными значениями искажен в одном и том же направлении, то такой ряд ошибок называется систематическим и односторонним по знаку. Систематические ошибки периодического характера соответственно изменяют знак и величину. Подобные ошибки возникают, например, при измерении углов теодолитом, в котором имеется эксцентриситет алидады. Если при многократных измерениях ошибки остаются неизменными как по абсолютному значению, так и по знаку, то такие ошибки называются постоянными. Так при многократном измерении угла теодолитом имеет место одна и та же ошибка за центрировку. При измерении линий больше длины мерной ленты возникает постоянная ошибка одинаковая на каждом уложении ленты. Постоянная ошибка является частным выражением систематической ошибки.Знание причин возникновения систематических ошибок позволяет заранее принять меры по исключению их из результатов измерений или уменьшению. Систематические ошибки характерны тем, что поддаются учету. Они могут быть исключены или сведены к минимуму путем тщательной проверки измерительных приборов, изменением методики измерений, предупреждением влияния внешних факторов. Но несмотря на это общая ошибка всегда содержит остаточную часть систематической ошибки, хотя она и мала по сравнению со случайной ошибкой. В ряду измерений всегда имеется остаточная часть ошибки. Случайными называют ошибки, размер и влияние которых на результат измерения неизвестны, величину и знак их заранее определить нельзя. Случайная величина – это переменная величина, конкретное значение которой зависит от случая, она может быть, а может и не быть. Случайными ошибки называют потому, что в ряду измерений каждая последующая ошибка по абсолютной величине может быть больше или меньше предыдущей, иметь знак плюс или минус и по предыдущим членам такого ряда нельзя установить, какой именно будет следующий за ним член ряда. Тем не менее, случайные ошибки подчинены статистическим закономерностям, называемых свойствами. Чем больше число измерений войдет в ряд их, тем резче выявится статистическая закономерность. Знание свойств дает возможность получить наиболее надежный результат из ряда (нескольких) измерений, а также оценить его точность.

2.2. Свойства случайных ошибок.В результате анализа многократных измерений выявлено, что как бы ни был велик ряд ошибок измерений, эти ошибки колеблются в определенных довольно узких пределах. Величина этого предела определяется условиями, в которых производятся измерения (прибор, исполнитель, погода, характер местности и др.). 1. Первое свойство. Случайные ошибки по абсолютной величине не могут превышать некоторого предела, называемого предельной ошибкой. Это свойство позволяет обнаруживать грубые ошибки в результатах измерений и исключать их. 2. Второе свойство. Положительные и отрицательные случайные ошибки равновозможны, т.е. примерно одинаково часто встречаются в ряду измерений. Это свойство позволяет выявлять систематические ошибки и учитывать их. 3.Третье свойство. Большие по абсолютной величине ошибки в ряду измерений встречаются реже, чем малые. Это свойство позволяет определить практический предел, который не могут превосходить случайные ошибки при данных условиях измерений. 4. Четвертое свойство. Среднее арифметическое из случайных ошибок измерений одной и той же величины, выполненных при одинаковых условиях, при неограниченном возрастании их числа есть величина малая и стремится к нулю. Оно является следствием первых двух свойств и проявляется при сложении ошибок. Это свойство называют свойством компенсации. На этих четырех свойствах случайных ошибок основывается вся теория ошибок измерений. Когда случайные ошибки ряда измерений обладают всеми перечисленными свойствами, то это называют нормальным распределением ошибок измерений.

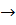
Свойство компенсации записывают так: ℓim {[D]/n} (3) при n , т.е., предел частного от деления суммы случайных ошибок на их число стремится к нулю с возрастанием числа измерений.

3. Арифметическая срединаНа основе четвертого свойства случайных ошибок установлен принцип получения из ряда измерений одной и той же величины наиболее надежного результата, наиболее близкого к истинному, наиболее точного. Его называют вероятнейшим значением. Если некоторая величина Х измерялась многократно, n раз, то в результате получился ряд численных значений ℓ₁ , ℓ₂ ,…, ℓ_n (4) причем, в этом ряду отсутствуют грубые, постоянные, систематические и односторонне действующие ошибки, то в таком ряду будет проявляться статистическая закономерность. Образуем ошибки

Х - ℓ₁ = D₁ Х - ℓ₂ = D (5) Х - ℓ_n = D_n

Сложим левые и правые части равенств, получим n X – [ℓ= [D]. При сложении положительные ошибки компенсируются отрицательными и сумма ошибок будет всегда небольшой, как бы ни возрастало их число. Найдем из этого выражения Х: Х = [ℓ]/n + [D]/n. Допустим, что число измерений неограниченно велико, тогда [D]/n = 0 и Х = [ℓ]/n. Так как число измерений всегда ограниченно, то в общем случае Х ≠ [ℓ]/n и можно записать [ℓ]/n – Х = , где - малая величина, имеющая своим пределом нуль при n .Поэтому общепринятообозначать [ℓ]/n = (6) и называть среднее арифметическое или арифметическая средина. Т.е., арифметическая средина – это частное от деления суммы значений измеренной величины на число измерений. Арифметическую средину принимают за окончательное, наиболее надежное, вероятнейшее значение измеренной величины при данных условиях и не только при значительном числе измерений, но и при конечном их числе, больше одного. Точность окончательного результата будет тем выше, чем больше число измерений n.

4. Средняя квадратическая ошибкаТак как истинноезначение измеренной величины неизвестно, то в качестве результата измерения принимают арифметическую средину и относительно ее вычисляют ошибки измерения и в отличие от истинных ошибок, их обозначают буквой δ. В геодезических измерениях характеристикой точности отдельного измерения принимается средняя квадратическая ошибка, обозначается m, которая для истинных ошибок вычисляется по формуле Гаусса m = (7) где D = Х - ℓ – истинные ошибки; ℓ - величина отдельного измерения. Эту формулу предложил и использовал К.Ф.Гаусс (1777 -1855) для оценки точности выполненных им геодезических измерений. Она может быть применена, когда известно истинное значение измеряемой величины. Но такие случаи в практике встречаются крайне редко. Поскольку на практике окончательным значением измеренной величины принимают арифметическую средину, то в качестве ошибок принимают отклонения от нее каждого измерения δ_I = ℓ_I - , при этом должно соблюдаться равенство нулю суммы ошибок [δ] = 0. Их называют вероятнейшимиошибками. Так как одно измерение не позволяет оценить точность, то среднюю квадратическую ошибку одного измерения подсчитывают по формуле Бесселя (1784-1846) m = 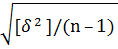, … (8) Оценке подлежит и точность самой арифметической средины. Она, естественно, будет выше точности отдельного измерения. Средняя квадратическая ошибка М арифметической средины определяется по формуле М = m/ (9) где m – средняя квадратическая ошибка, вычисленная по формуле Гаусса (7) или Бесселя (8). Средние квадратические ошибки, вычисленные по формулам Гаусса и Бесселя считают абсолютными. Средняя квадратическая ошибка является хорошим показателем точности измерений и достоинства данного ряда измерений, а также характеристикой условий, в которых произведены измерения. Средняя квадратическая ошибка обладает следующими особенностями: 1) на ее величину влияют преимущественно большие по абсолютной величине случайные ошибки, которые и определяют собой степень надежности полученных результатов измерений; 2) она устойчива, поэтому достаточно небольшого числа измерений для определения ее величины с удовлетворительной степенью точности; 3) по ней можно судить о предельной ошибке возможной при аналогичных условиях измерений.

5. Средняя ошибкаВ некоторых случаях точность геодезических измерений характеризуют средней ошибкой. Средней ошибкой называется среднее арифметическое из абсолютных значений случайных ошибок равноточных измерений, ее обозначают буквой θ: θ = [|δ|]/n (10 ) Это абсолютная ошибка. Средняя ошибка удобна тем, что для ее вычисления не нужно ни возводить в квадрат, ни извлекать корень.

Между средней и средней квадратической ошибками имеется математическая зависимость m = 1,25 θ; θ = 0,8m (11)

6. Вероятная ошибкаИногда точность измерений оценивают вероятной ошибкой. Вероятной ошибкой называется такое значение случайной ошибки, по отношению к которому при данных условиях измерения одинаково возможна ошибка как больше этого значения по абсолютной величине, так и меньше его. Она расположена в середине ряда ошибок измерения, составленному по возрастанию или убыванию их (занимает срединное положение. Обозначается через r и принимается в качестве меры точности измерений наряду со средней квадратической и средней ошибками (она служит мерой точности измерений в США). В случае нормального распределения ошибок вероятная ошибка составляет примерно две трети средней квадратической ошибки: r = 0,6745 m или приближенно r ≈ ⅔ m. Ошибки - средняя квадратическая, средняя, истинная, вероятная и предельная являются абсолютными. Их выражают в единицах измеряемой величины.

7. Относительная ошибкаВ качестве критерия точности линейных измерений кроме абсолютных ошибок определяют также относительные ошибки. Относительной ошибкой называется отношение абсолютной ошибки (средней квадратической) к полученному среднему значению измеренной величины. Нередко она называется точностью измерения. Она выражается в виде простой дроби, числитель которой единица, а знаменатель – число, округленное до двух-трех значащих цифр с нулями, получаемое делением средней квадратической ошибки на измеренную величину. Чтобы получить в числителе единицу надо разделить измеренную величину на среднюю квадратическую ошибку и в знаменателе получим значение относительной ошибки. Для двойных измерений относительная ошибка получается делением среднего значения измеренной величины на разность двух измерений d 1/N = m/ℓ или 1/N = 1/( ℓ :d) (12) Например, относительная ошибка измеренной линии длиной 110м с расхождением между прямым и обратным результатами 5см будет: 1/N = 5см/110м = 1/(110м:0,05м) =1/2200. Ошибки измерения длин линий зависят от значения измеряемой величины. В наименовании относительной ошибки обычно указывают и название соответствующей ей абсолютной ошибки: средняя квадратическая относительная ошибка; средняя относительная ошибка; вероятная относительная ошибка; истинная относительная ошибка; предельная относительная ошибка.

8. Предельная ошибкаПредельной ошибкой называется допустимый предел, т.е. величина ошибки, больше которой ошибка считается грубой. В строительных нормах и геодезических измерениях предельная ошибка называется допустимым отклонением или допуском.При нормальном распределении ошибок найдено теоретически и подтверждено опытным путем правило, что при значительном числе измерений абсолютная величина случайной ошибки в ряду измерений не превосходит утроенной средней квадратической ошибки: D_пред = 3m (13) Ошибки геодезических измерений входят составной частью в общие ошибки строительных и других работ. Поэтому, чтобы ошибки геодезических измерений существенно не влияли на общую ошибку, их выполняют с повышенной точностью и за предельную принимают удвоенную среднюю квадратическую ошибку D_пред = 2m. (14) Измерения, ошибки которых превышают предельные значения (допуск), считают грубыми и бракуют. Такие измерения выполняют заново. В геодезических измерениях установлены предельные ошибки (допуски): в линейных измерениях технической точности предельная относительная ошибка, вычисленная как D_пред /ℓ, принимается равной 1:2000; в угловых измерениях предельная абсолютная ошибка измерения угла принимается равной удвоенной точности отсчета по угломерной шкале D_пред = 2t; при нивелировании технической точности разность измеренного превышения по двум сторонам рейки допускается равной половине наименьшего деления шкалы рейки (по рейкам с сантиметровыми делениями 5мм). Критерий предельной ошибки обоснован теорией ошибок измерений, в которой доказывается, что из общего числа ошибок данного ряда измерений 68,3 % ошибок находятся в интервале от 0 до m, в интервале от 0 до 2m находятся 95,4 % ошибок, а в интервале от 0 до 3m находятся 99,7% ошибок. То есть, из 100 ошибок данного ряда измерений лишь 5 могут оказаться больше или равны 2m, а из 1000 ошибок только три могут быть больше или равны 3m.

9. Двойные измеренияВ практике, для контроля измерений, для выявления грубых ошибок и повышения точности определяемую величину, как правило, измеряют не менее двух раз. Такие измерения называют двойными. С целью выявления грубых ошибок все геодезические измерения выполняют с контролем, не менее двух раз: углы измеряют при двух положениях теодолита; длины линий - в прямом и обратном направлениях; превышения между точками - по двум сторонам рейки и в прямом и обратном ходах. За окончательное значение принимают среднее из двух измерений, если расхождение между ними не превышает установленного предела – допуска. Это значение будет наиболее надежным, наиболее точным. Разности двойных измерений считают истинными ошибками. Оценку точности двойных измерений производят по формуле m = (15) где m – ср. кв. ошибка одного измерения; d – разность между результатами двух измерений; n – число разностей. Средняя квадратическая ошибка среднего результата из двух измерений вычисляется по формуле М = ½ (16)

10. Оценка точности функций измеренных величин Если определяемая величина является функцией других непосредственных измерений, например, u = f(x,y,z,…t), то возникает необходимость вычисления средней квадратической ошибки функции измеренных величин. Рассмотрим простую линейную функцию вида z = x +y, где x и y – независимые переменные аргументы. Предположим, что каждый из этих аргументов измерялся n раз и каждое измерение сопровождалось случайными ошибками ∆х_i и ∆y_i (i = 1,2,3,…n), тогда ∆z_i = ∆х_i + ∆y_i Для перехода к средним квадратичеким ошибкам возведем обе части равенства в квадрат, просуммируем полученные выражения и разделим на число измерений n, получим [∆z² ]/n =( [∆x²]/n +[∆y ²]n + 2[∆x ∆y])/n. На основании того, что предел суммы ошибок деленное на их число при n стремящемся к бесконечности равен нулю ℓim {[D]/n} = 0 при n , последний член правой части равенства равен нулю [∆x ∆y ]/n = 0. Отбрасывая его и переходя к средним квадратическим ошибкам, получим m_z² = m_x² + m_y² (17) Формула справедлива и для равенства z = x – y. Обобщая, для функции вида z = x ± y ± t ± u± …± v формула средней квадратической ошибки будет иметь вид m_z² = m_x² + m_y² + m_t² + m_u² + …+ m_v² (18 ) т.е., квадрат средней квадратической ошибки алгебраической суммы или разности многих аргументов равен сумме квадратов средних квадратических ошибок слагаемых. Если средние квадратические ошибки аргументов равны между собой m_x = m_y= m_t + m_u + … + m_v =m, то формула (18) примет вид m_z = m (19) т.е., средняя квадратическая ошибка суммы n измеренных величин с равными средними квадратическими ошибками в 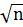раз больше средней квадратической ошибки одного слагаемого.

11. Порядок оценки точности результатов многократных измеренийТочность результатов многократных измерений одной и той же величины оценивают в такой последовательности: 1.Находят вероятнейшее (наиболее точное для данных условий) значение измеренной величины по формуле арифметической средины х = [ℓ]/n. 2. Вычисляют отклонения δ = ℓ_i – каждого значения измеренной величины от значения арифметической средины. Подсчитывают число ошибок с разными знаками и их суммы. Контролем правильности вычислений служит равенство нулю суммы отклонений [δ] = 0. Может быть незначительное отличие от нуля за счет округления чисел. 3. По формуле Бесселя (8 ) вычисляют среднюю квадратическую ошибку одного измерения m = . 4. Вычисляют среднюю квадратическую ошибку арифметической средины М = m/ . 5. Для измеренной линейной величины вычисляют относительную среднюю квадратическую ошибку каждого измерения и арифметической средины 1/N = m/ℓ и М = m/ 6.При необходимости подсчитывают предельную ошибку одного измерения D_пред = 2m, которая может служить допустимым значением ошибок аналогичных измерений.

Тема 2. Неравноточные измерения