Билет №38. Найти перпендикуляр к двум непараллельным прямым.

М1(х1,у1,z1)

a1(m1,n1,p1)

 

 

M2(x2,y2,z2)

 

 

a2(m2,n2,p2)

 

а = а1*а2

(а*а1)*(М1М)=0 Задаём вектор нормали как векторное произведение

(а*а2)*(М2М)=0

 

x-x1 y-y1 z-z1

m1 n1 p1 = 0

n1 p1 p1 m1 m1 n1

n2 p2 p2 m2 m2 n2

 

x-x2 y-y2 z-z2

m2 n2 p2 = 0

n1 p1 p1 m1 m1 n1

n2 p2 p2 m2 m2 n2

 

Билет №40. Расстояние между скрещивающимися прямыми.
(над a1, a2 и r ставить значок вектора)

a1 и a2 – направляющие вектора, m,n,p – их координаты, x,y,z – координаты нормалей к каждой из прямых

Известно, что длина общего перпендикуляра скрещивающихся прямых равна расстоянию между этими прямыми.

Теорема: Расстояние между двумя скрещивающимися прямыми равно расстоянию между параллельными плоскостями, проходящими через эти прямые.

Следующая теорема дает один из способов нахождения расстояния и угла между скрещивающимися прямыми.

Расстояние между скрещивающимися прямыми равно расстоянию от точки, являющейся проекцией одной из данных прямых на перпендикулярную ей плоскость, до проекции другой прямой на эту же плоскость.

 

(x-x1)/m1 = (y-y1)/n1 = (z-z1)/p1

(x-x2)/m2 = (y-y2)/n2 = (z-z2)/p2

a1 = (m1,n1,p1) a2 = (m2,n2,p2)

r = (x2-x1, y2-y1, z2-z1)

((a1*a2)*r)/|a1*a2| = m1 n1 p1
m2 n2 p2 / (n1p2-n2p1)^2+(m2p1-m1p2)^2+(m1n2-m2n1)^2
x2-x1 y2-y1 z2-z1

На практике чаще всего концы общего перпендикуляра неизвестны, поэтому используют другой подход. Через две скрещивающиеся прямые можно провести параллельные плоскости, и расстояние между данными плоскостями равно расстоянию между данными прямыми. В частности, между этими плоскостями и торчит общий перпендикуляр.

В курсе аналитической геометрии из вышесказанных соображений выведена формула нахождения расстояния между скрещивающимися прямыми:
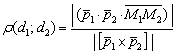(вместо наших точек «эм один, два» можно взять произвольные точки прямых).

 

 

Билет №41. Найти уравнение перпендикуляра из точки на прямую в пространстве.

m1(x-x0) + n1(y-y0) + p(z-z0) = 0

 

x = x1+m1*t
y = y1+n1*t
z = z1+p1*t

 

m1(x1-x0+m1*t) + n1(y1-y0+n1*t) + (z1-z0+p1*t) =>

 

t = (m1(x0-x1) + n1(y0-y1) + p1(z0-z1))/(m1^2 + n1^2 + p1^2)

Пересечение плоскости с перпендикулярной прямой к плоскости, проходящей через прямую и точку, даст нам искомый перпендикуляр.

 

 

Билет №39. Расстояние от точки до прямой.

Определение.

Расстояние от точки до прямой— равно длине перпендикуляра, опущенного из точки на прямую.