Выборочное наблюдение
1.Понятие о выборочном наблюдении. Виды выборки.
2.Расчет ошибки выборки и распространение ее на генеральную совокупность.
3.Определение необходимой численности выборки.
j. Выборочное наблюдение получило в настоящее время достаточно широкое распространение не только в экономических исследованиях. Оно является основным в социологических исследованиях, доминирующим в различных областях знаний: медицине, юриспруденции, метрологии и многих других. Причин его применения несколько:
1. Как это ни странно звучит, но применение выборочного метода способствует повышению точности данных. Происходит это за счет того, что с уменьшением числа единиц наблюдения –резко снижаются ошибки регистрации.
2. Применение выборок обеспечивает экономию материальных, трудовых, финансовых ресурсов и времени.
3. Без выборки не обойтись, когда наблюдение связано с порчей объектов, например, при изучении качества продукции на испытаниях.
Методы описательной статистики включают сбор данных их обработку и анализ по всем единицам изучаемой совокупности, которая в случае отбора из нее части единиц называется генеральной совокупностью. Генеральная совокупность может быть реальной, а может быть и гипотетической, т.е. включающей несуществующие случаи или возможные результаты эксперимента. Совокупность отобранных единиц из генеральной совокупности называется выборочной совокупностью.
Для того чтобы по выборке можно было судить о свойствах генеральной совокупности, выборка должна быть репрезентативной (представительной), т.е. она должна полно и адекватно представлять свойства генеральной совокупности. Репрезентативность данных может быть обеспечена только при объективности отбора данных.
Выделяют следующие виды отбора: случайный, отбор единиц по определенной схеме, сочетание первого и второго способа.
В математической статистике обязательно водят деление выборки на повторную и бесповторную. Первая соответствует схеме возвратного шара, вторая – безвозвратного. В социально-экономических исследованиях нет смысла применять повторную выборку, поэтому как правило имеется в виду бесповторный отбор. При любом виде выборки отбор производится тремя отмеченными способами отбора.
При случайном отборе прежде всего составляется список единиц совокупности, в которой каждой единице присваивается цифровой код (номер). Затем производится жеребьевка. Выпавшие номера соответствуют единицам, попавшим в выборку (число номеров заранее запланировано). Но жеребьевка с использованием технических средств не совсем надежна, а считается более надежным отбор по таблице случайных чисел. Такие таблицы есть в любом учебнике математической статистики, некоторых учебниках по общей теории статистики, математических справочниках.
Отбор единиц в соответствии с принятой схемой может быть типическим, серийным (гнездовым), механическим.
При типическом отборе вся генеральная совокупность разбивается на группы (типы, районы) однородные в качественном отношении, а затем внутри каждой такой группы производится случайный отбор подлежащих наблюдению единиц.
При серийном отборе в качестве единицы отбора представлена серия единиц («гнездо»), выбранных случайно, внутри которой проводится сплошное наблюдение.
При механическом отборе (очень распространенный способ) отбираются единицы с установленным шагом отбора, например, каждый пятый, десятый, сотый.
k. После проведения отбора выборочной совокупности, необходимо рассчитать его обобщающие характеристики (среднюю или долю), затем рассчитать ошибку выборки, скорректировать ее в зависимости от требуемой или желаемой вероятности и распространить на всю генеральную совокупность.
Для удобства введем условные обозначения, которые являются общепринятыми в общей теории статистики и математической статистике:
N – объем генеральной совокупности (число входящих в нее единиц).
n – объем выборочной совокупности (число единиц, пропавших в выборку.
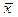- генеральная средняя ( среднее значение признака в генеральной совокупности).
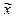- выборочная средняя (среднее значение признака в выборочной совокупности)
р – генеральная доля (доля единиц, обладающих данным признаком в генеральной совокупности).
w – выборочная доля (доля единиц, обладающих данным признаком в выборочной совокупности).
(1-w) – доля единиц не обладающая признаком в выборке
w(1-w) – дисперсия доли в выборке.
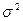- генеральная дисперсия (дисперсия признака в генеральной совокупности).
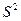- выборочная дисперсия (дисперсия признака в выборочной совокупности)
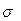- среднее квадратическое отклонение признака в генеральной совокупности.
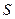- среднее квадратическое отклонение признака в выборочной совокупности.
Расчет обобщающих характеристик в выборке: 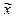, ,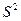w производится по уже известным вам формулам из предыдущих тем.
Ошибка выборки для средней находится:
при повторном отборе:
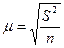
при бесповторном отборе:
Ошибка выборки для доли находится:
при повторном отборе:
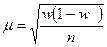
при бесповторном отборе:
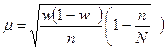
Величина ошибки выборки зависит от вариации признака в выборке и объема выборки. Для того чтобы определить предельную ошибку выборки (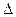 
)необходимо увеличить ошибку выборку в зависимости от требуемой доверительной вероятности. Чем с большей вероятностью мы хотим узнать наступление события тем больше будет величина предельной ошибки выборки. Предельная ошибка выборки находится по формуле:
где t – коэффициент доверия, который можно определить по следующей таблице:
| Коэффициент доверия,t | 1,00 | 1,96 | 2,00 | 2,58 | 3,00 |
| Вероятность, Ф(t) | 0,683 | 0,950 | 0,954 | 0,990 | 0,997 |
Необходимо заметить, что в экономических исследованиях коэффициент доверия больше 2,00, как правило, не используется.
Данная формула предельной ошибки выборки используется как для повторного так и для бесповторного отбора, как для увеличения ошибки выборки для средней так и для доли.
После нахождения предельной ошибки выборки ее необходимо распространить на всю генеральную совокупность. Для этого определяются пределы генеральных характеристик:
для генеральной средней:
= 
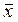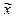
для генеральной доли:
р = w
l.Уже на стадии организации выборочного наблюдения приходится решать вопрос о том, каков должен быть объем выборочной совокупности, чтобы была обеспечена требуемая точность результатов наблюдений. Для того чтобы его рассчитать необходимо иметь следующие данные:
1. Размер доверительной вероятности (Р), по которому мы определим коэффициент доверия (t).
2. Дисперсию признака ( 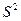)или доли (w(1-w)) в выборке .
3. Величину максимально допустимой ошибки (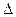предельной ошибки выборки).
4. Объем генеральной совокупности (N).
Если 1 и 3 показатели задаются исследователем, а 4 как правило известен, дисперсия признака и доли в выборке неизвестна.
Для нахождений дисперсий используют приближенные способы оценки:
1. Можно провести «пробное» обследование (обычно небольшого объема), на базе которого определяется величина дисперсии. Если проведено несколько пробных обследований, то выбирается наибольшая величина.
2. Можно использовать данные прошлых выборочных обследований, проводившихся в аналогичных целях.
3. Если распределение признака в генеральной совокупности может быть отнесено к нормальному закону распределения, то размах вариации (R = X max – X min) для количественного признака) примерно равен R =6 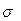, отсюда 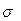= 1/6 R.
При проведении социально-экономических исследований, как правило, можно с достаточной точностью указать максимально и минимально возможные значения.
Приведем формулы, используемые для определения численности выборки (n):
При повторном отборе для средней:
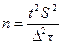
При бесповторном отборе для средней:
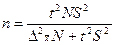
Для доли при повторном отборе:
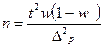
Для доли при бесповторном отборе:
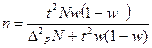
В случаях когда частость w даже приблизительно неизвестна, в расчет вводят максимальную величину дисперсии доли, равную 0,25 (то еcть , при равенстве w и (1-w)).
Литература:
Основная:1.2.3,5,7,
Дополнительная: 11.12.14
Задания для СРС:
1.В чем преимущества выборочного метода в сравнении с другими видами статистических наблюдений?
2. Что такое ошибка выборки (репрезентативности)? Какие факторы определяют ее величину?
3. Чем отличается величина ошибки выборки при повторном и бесповторном отборе? Какая из этих ошибок больше?