II закон Ньютона.
ОПРЕДЕЛЕНИЕ: Ускорение всякого тела прямо пропорционально действующей на него силе и обратно пропорционально массе тела:  .
.
Этот закон, также как и I закон Ньютона справедлив только в инерциальных системах отсчета.
 В частном случае, при отсутствии воздействия на тело со стороны других тел (F = 0) ускорение a = 0, что совпадает с утверждением I закона Ньютона. Поэтому первый закон, казалось бы, входит во второй как его частный случай. Несмотря на это, I закон формулируется независимо от II закона, т.к. в нем, по сути, заключен постулат о существовании инерциальных систем отсчета.
В частном случае, при отсутствии воздействия на тело со стороны других тел (F = 0) ускорение a = 0, что совпадает с утверждением I закона Ньютона. Поэтому первый закон, казалось бы, входит во второй как его частный случай. Несмотря на это, I закон формулируется независимо от II закона, т.к. в нем, по сути, заключен постулат о существовании инерциальных систем отсчета.
Уточняя предыдущую формулу можно записать
 .
.
В данном случае единицу силы можно выбрать так, что k = 1, т.е.
 – основное уравнение классической механики
– основное уравнение классической механики
В соответствии с этой формулой за единицу силы следует принять силу, которая массе 1кг сообщает ускорение 1м/с2. Эта единица называется ньютон: 1Н=1кг×1 м/с2. Размерность силы: [F]=  ; (1кГ=9,81Н).
; (1кГ=9,81Н).
II закон Ньютона можно записать в скалярной форме, взяв проекции силы на координатные оси X, Y и Z.
Важным положением динамики является принцип независимости действия сил. На практике на тело может действовать одновременно несколько сил:  ,
,  , …
, …  . И данный принцип гласит, что каждая из сил, действующих на тело, сообщает ему ускорение, подсчитываемое по основному уравнению механики, независимо от того действуют на него другие силы или нет, двигалось тело или покоилось. Согласно этому можно записать:
. И данный принцип гласит, что каждая из сил, действующих на тело, сообщает ему ускорение, подсчитываемое по основному уравнению механики, независимо от того действуют на него другие силы или нет, двигалось тело или покоилось. Согласно этому можно записать:

 , где
, где  – результирующая сила.
– результирующая сила.
II закон Ньютона можно записать и в другом виде.
Пусть на тело массой «m» в течение некоторого промежутка времени Dt, двигавшееся со скоростью  подействовала постоянная сила
подействовала постоянная сила  . Она будет сообщать телу постоянное ускорение
. Она будет сообщать телу постоянное ускорение 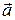 , в связи, с чем к концу промежутка времени тело приобретет скорость
, в связи, с чем к концу промежутка времени тело приобретет скорость 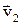 . Тогда, согласно второму закону Ньютона можно записать
. Тогда, согласно второму закону Ньютона можно записать
 .
.
Величину  называют импульсом тела (старое название «количество движения»). Направление вектора
называют импульсом тела (старое название «количество движения»). Направление вектора  совпадает с направлением вектора
совпадает с направлением вектора  . Имеем
. Имеем  , где
, где  – изменение вектора импульса тела.
– изменение вектора импульса тела.
ОПРЕДЕЛЕНИЕ: Изменение вектора импульса тела со временем равно результирующей всех сил, действующих на тело (закон изменения импульса тела).
Если сила  переменна, то при Dt®0 получаем
переменна, то при Dt®0 получаем  – это более общее выражение II закона Ньютона, верное и для больших скоростей, когда масса начинает быстро расти по закону
– это более общее выражение II закона Ньютона, верное и для больших скоростей, когда масса начинает быстро расти по закону  .
.
Добавим, что величину  называют импульсом силы.
называют импульсом силы.
Тогда, если силу, действующую на тело в течение малого промежутка времени можно практически считать постоянной, то закон изменения импульса можно записать в виде:
ОПРЕДЕЛЕНИЕ: Импульс силы, действующей на тело в течение малого промежутка времени, равен изменению импульса тела (или изменению количества движения).
Замечание: Основной закон динамики (II закон Ньютона) используется для решения основной задачи динамики, которая кратко формулируется так: требуется определить закон движения материальной точки, если известны действующие на нее силы. Логика решения такова: определив ускорение, с помощью известных формул кинематики ищутся выражения для скоростей и координат.