Гипербола

Гиперболой называется множество всех точек плоскости, модуль разности расстояний от каждой из которых до двух заданных точек и этой же плоскости, называемых фокусами, есть величина постоянная, меньшая, чем расстояние между фокусами.

Каноническое уравнение гиперболы:

, (6)

где 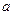— действительная, 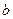— мнимая полуось гиперболы. Числа и — соответственно действительная и мнимая оси гиперболы. Для гиперболы (6):

1) координаты фокусов: , , где — половина расстояния между фокусами (см. рис);

2) числа 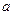, 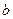и связаны соотношением

; (7)

3) расстояние между фокусами равно ;

4) точки и называются вершинами гиперболы , точка — центром гиперболы;

Эксцентриситетом гиперболы называется число:

5) ( , т.к. ). (8)

Прямоугольник, центр которого совпадает с точкой , а стороны равны и параллельны осям гиперболы, называется основным прямоугольником гиперболы.

Диагонали основного прямоугольника гиперболы лежат на двух прямых, называемых асимптотами гиперболы; они определяются уравнениями

6) (9)

Две прямые и (см. рисунок), параллельные мнимой оси гиперболы и отстоящие от неё на расстоянии, равном , называются директрисами гиперболы; они определяются уравнениями

7) . (10)

Уравнение или (11)

также является уравнением гиперболы, но действительной осью этой гиперболы служит отрезок оси длины .

Гипербола, задаваемая уравнением (11), называется сопряжённой гиперболе (6)

Пример 5.3. Составьте уравнение гиперболы, если её фокусы лежат на оси 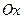и расстояние между ними равно 10, а длина мнимой оси равна 8.

По условию, ; . Тогда по формуле (7) получим:

.

Тогда уравнение гиперболы:

.

Уравнения

, также задают гиперболу, координаты центра которой задаются точкой .