Окружность

Окружностью называется множество всех точек плоскости, удаленных от заданной точки этой же плоскости на одно и тоже расстояние . Точка называется центром, а — радиусом окружности.

В прямоугольной системе координат уравнение окружности имеет вид

, (1)

где — координаты её центра, — радиус окружности.

В частности, если центр окружности совпадает с началом координат, т.е. , , то уравнение (1) примет вид:

(2)

Пример 5.1. Найдите координаты центра и радиус окружности .

Разделив уравнение на 2, и сгруппировав члены уравнения, получим . Дополним выражения и до полных квадратов, прибавив к первому двучлену 4 , а ко второму (одновременно к правой части прибавляется сумма этих чисел):

.

По формуле (1) имеем , , т.е. — координаты центра окружности; — радиус окружности.

Эллипс

Эллипсом называется множество всех точек плоскости, сумма расстояний от каждой из которых до двух данных точек и этой же плоскости, называемых фокусами эллипса, есть величина постоянная и большая, чем расстояние между фокусами.

Каноническое уравнение эллипса:

, (3)

 

где 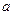— большая полуось, 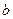— малая полуось эллипса.

v Если , то:

1) координаты фокусов: , , где — половина расстояния между фокусами (см. рис);

2) числа 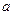, 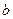и связаны соотношением

; (4)

3) расстояние между фокусами равно ;

Форма эллипса характеризуется его эксцентриситетом.

Эксцентриситетом эллипса называется отношение фокусного расстояния (расстояния между фокусами) к большой оси :

4) ( , т.к. ); (5)

Директрисами эллипса называются прямые и параллельные малой оси эллипса и отстоящие от неё на расстоянии, равном ;

5) и — уравнения директрис.

v Если , то уравнение (3) определяет окружность .

 

Пример 5.2. Дано уравнение эллипса . Найдите длины его полуосей, координаты фокусов, эксцентриситет эллипса.

Запишем уравнение эллипса в виде (3), разделив обе его части на 1176:

.

Отсюда , .

Используя соотношение (4), находим и . Следовательно, и .

По формуле (5) находим .