Элементарные преобразования матрицы

Рассмотрим матрицу .

Выделим в матрице 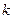строк и 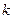столбцов, где 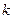— число меньшее или равное наименьшему из чисел и .

Определителем, порожденным матрицей называется определитель порядка 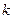, составленный из элементов, стоящих на пересечении 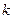строк и 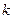столбцов.

Например, пусть , . Тогда , — определители второго порядка, порожденные матрицей .

Пусть . Тогда — определитель третьего порядка, порожденный данной матрицей.

Рангомматрицы называется наибольший из порядков определителей, отличных от нуля, порожденных данной матрицей. Обозначается или .

Ясно, что если равны нулю все определители порядка 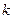, порожденные данной матрицей, то ранг матрицы меньше 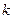. Действительно, по определению, каждый из определителей -го порядка выражается линейно через определители 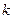-го порядка. Значит, все определители -го порядка равны нулю. Аналогично доказывается, что равны нулю все определители -го и более высоких порядков. Отсюда следует, что ранг матрицы меньше .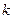

Теорема. Ранг матрицы не изменится, если:

а) все строки заменить столбцами;

б) поменять местами две строки (два столбца);

в) умножить каждый элемент строки (столбца) на один и тот же множитель, отличный от нуля;

г) прибавить к элементам одной строки (столбца) соответствующие элементы другой строки (другого столбца), умноженные на один и тот же множитель.

Преобразования а) — г) называются элементарными.

Эквивалентными называются матрицы и , если одна из другой получаются с помощью элементарных преобразований. Эквивалентность матриц и обозначают следующим образом: ~ .

Пример 1.13. Определите ранг матрицы : .

Приведём матрицу к ступенчатому виду с помощью элементарных преобразований:

~ ~ ~ ,

, т.е. .