Теория.

Лабораторная работа № 1

 

Тема: «Решение систем линейных уравнений методом Гаусса»

 

Вариант 4

 

Выполнил:

студент гр. Б3-832-1 Матросов Н.С.

 

Проверил:

Рычина Н.А.

 

 

Дана система линейных уравнений Ах = В.

1.Решить данную систему методом Гаусса.

В случае, если максимальная по модулю компонента невязки больше 10^-4, произвести уточнение решения тем же методом.

2.Используя прямое преобразование метода Гаусса, найти

a. det A;

b. A^-1.

3.Вычислить число обусловленности cond A в различных простых нормах и охарактеризовать чувствительность данной системы к погрешностям исходных данных.

Сделать выводы по работе.

Теория.

Дана система линейных уравнений:

 

Будем считать, что , так как мы всегда можем этого добиться перестановкой местами уравнений системы. Исключим неизвестную переменную x₁ из всех уравнений системы, начиная со второго. Для этого ко второму уравнению системы прибавим первое, умноженное на - 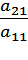, к третьему уравнению прибавим первое, умноженное на - 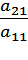, и так далее, к n-ому уравнению прибавим первое, умноженное на - . Система уравнений после таких преобразований примет вид:

 

 

где

 

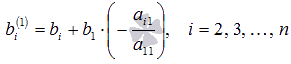
Будем считать, что . Приступаем к исключению неизвестной переменной x₂ из всех уравнений, начиная с третьего.

Для этого к третьему уравнению системы прибавим второе, умноженное на , к четвертому уравнению прибавим второе, умноженное на , и так далее, к n-ому уравнению прибавим второе, умноженное на . Система уравнений после таких преобразований примет вид

 

 

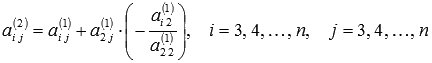
где

 

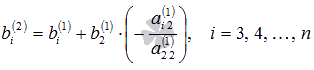
Таким образом, переменная x₂ исключена из всех уравнений, начиная с третьего.

Так продолжаем прямой ход метода Гаусса пока система не примет вид

С этого момента начинаем обратный ход метода Гаусса: вычисляем x_n из последнего уравнения как 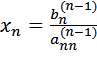, с помощью полученного значения x_n находим x_n-1 из предпоследнего уравнения, и так далее, находим x₁ из первого уравнения.

Для контроля точности при реализации метода Гаусса используют невязку:

ξ^о= Ах - В - разность между неточным и приближенным значением.

Применение метода Гаусса для нахождения определителей и обратной матрицы пользуются формулами:

det = 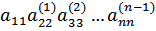Суть метода заключается в том, чтобы привести матрицу методом эквивалентных преобразований к треугольному виду и найти определитель.

А – А^-1 = Е

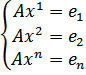
Суть метода заключается в том, чтобы подставляя единичные векторы в исходную матрицу найти соответствующие корни матрицы и по полученным данным составить обратную матрицу.

Нормой матрицы A(n,m) называют неотрицательное число, для которой выполняется следующее условие:

1) ||A||≥0, ||A||=0;

2) ||α·A||=|α|·||A|| ;

3) ||A+B||≤||A||+||B|| ;

4) ||A·B||≤||A||·||B||.

1. ||A||₁ =

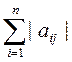
2. ||A||₂ =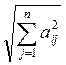

3. ||A||_∞ =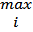

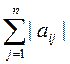
Выражение:

ν= cond A=||A||·||A^-1|| - называют числом обусловленности.

Обусловленность оценивает близость матрицы коэффициентов А к вырожденной.

Число обусловленности cond(A) является количественной оценкой обусловленности.