Дифференциал функции
Т.6. Необходимое и достаточное условие дифференцируемости функции в точке: ф-я 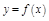 диф-ма в т.
диф-ма в т. 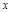 (т.е. имеет конечную производную)
(т.е. имеет конечную производную)  ее приращение в этой точке можно представить в виде
ее приращение в этой точке можно представить в виде  , где
, где  – б.м. более высокого порядка малости, чем
– б.м. более высокого порядка малости, чем  .
.
Д-во: 
 , тогда
, тогда  .
.



 .
. 
Пусть  диф-я в т. x, т. е.
диф-я в т. x, т. е.  .
.
Опр.1. Дифференциалом ф-и 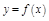 наз-ся главная, линейная относительно
наз-ся главная, линейная относительно  часть приращения ф-и:
часть приращения ф-и:  .
.
Зам. Вообще говоря,  . Но для
. Но для 
 . В частности для,
. В частности для,  .
.
Зам.  .
.
 Геометрический смысл дифференциала:
Геометрический смысл дифференциала:
Дифф-л ф-и в т. 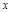 , соответствующий приращению
, соответствующий приращению  , есть приращение ординаты касательной к графику ф-и
, есть приращение ординаты касательной к графику ф-и 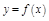 в т. с абсциссой
в т. с абсциссой 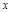 .
.
Свойства дифференциалов:
1)  ;
;
2)  ;
;
3)  ;
;
4)  ;
;
5)  .
.
Зам.В приближенных вычислениях используется, что  .
.
ПР.  ,
,  .
.