Производная сложной функции
Т.3. О дифференцированиии сложной функции: Если ф-я  диф-ма в т.
диф-ма в т. 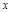 , а ф-я
, а ф-я  диф-ма в т.
диф-ма в т.  , то сложная ф-я
, то сложная ф-я  диф-ма в т.
диф-ма в т. 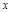 и
и  или
или  .
.
Д-во. Дадим аргументу 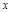 приращение
приращение  , тогда
, тогда  ,
,  . Ф-я
. Ф-я  имеет производную в т.
имеет производную в т. 


 или
или  .
. 
Зам. Условия достаточны, т.е. ф-и м.б. не диф-мы, а их композиция – диф-ма.
Сл.Пусть  и существуют производные в соотв. точках. Тогда
и существуют производные в соотв. точках. Тогда  .
.
ПР.  ;
;  .
.
_______________________________________________________