Скорости движения ведущей и свободной ветвей ремня различны, а следовательно различны и скорости рабочих поверхностей ведущего и ведомого шкивов.

Окружная скорость рабочей поверхности ведущего шкива всегда больше окружной скорости ведомого шкива (V₁ > V₂).

Отношение разности между окружными скоростями на рабочей поверхности ведущего и ведомого шкивов к скорости ведущего шкиве называюткоэффициентом скольжения передачи (x).

, (2.23)

где индекс «1» соответствует ведущему, а индекс «2» - ведомому шкивам.

Выражая в (2.23) линейные (тангенциальные) скорости рабочих поверхностей шкивов через угловую скорость и их радиус, нетрудно получить выражение, определяющее передаточное число ременной передачи через ее конструктивные параметры:

. (2.24)

Таблица 2.2. Рекомендуемые передаточные числа ременных передач Тип передачи Передаточное число u £ Плоскоременная 4…5 Клиноременная 6…8 Поликлиноременная

Рекомендуемые значения передаточных чисел фрикционных ременных передач представлены в табл. 2.2.

Тяговая способность и долговечность ремняявляются основными критериями работоспособности ременной передачи. Проектный расчет ременной передачи обычно выполняется по тяговой способности, а расчет долговечности при этом является проверочным. Проиллюстрируем поведение ременной передачи графиком, на котором по оси абсцисс отложен коэффициент тяги, а по оси ординат - коэффициент скольжения и КПД (рис. 2.4). На графике можно выделить три основных зоны:

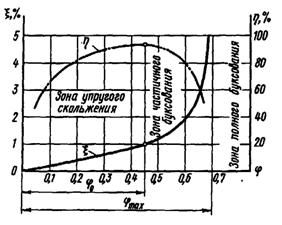Рис. 2.4. Кривые скольжения и КПД.

1 зона, где 0 £ j £ j₀, эту область называют зоной упругого скольжения;

2 зона, где j₀ £ j £ j_max, её называют зоной частичного буксования;

3 зона, где j > j_max, эту область называют зоной полного буксования.

В зоне упругого скольжения коэффициент скольжения растет линейно с увеличением коэффициента тяги, одновременно возрастает и КПД передачи, достигая максимального значения при оптимальной величине коэффициента тяги j₀. Дальнейшее увеличение коэффициента тяги приводит к частичному буксованию ремня, коэффициент скольжения растет нелинейно и намного интенсивнее по сравнению с 1 зоной, а КПД также нелинейно и интенсивно снижается. При достижении коэффициентом тяги величины j_max наступает полное буксование передачи (ведомый шкив останавливается), величина скольжения становится равной единице, а КПД падает до нулевого значения.

Представленный выше анализ показывает, что наиболее благоприятной для работы передачи является область коэффициентов тяги, прилегающая к его оптимальному значению, поскольку именно в этой области передача обладает максимальным КПД. При этом величина упругого скольжения для разных типов ремней лежит в пределах 1…2%, а КПД для передачи плоским ремнем можно принять равным 0,95…0,97, клиновым или поликлиновым – 0,92…0,96.

Напряжения в ремне. Напряжения, возникающие в ведущей ветви ремня от действия рабочих нагрузок, нетрудно определить, разделив (2.20) на площадь поперечного сечения ремня A_р,

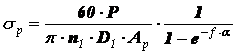. (2.25)

Кроме рабочих напряжений, обусловленных предварительным натяжением ремня и тяговым усилием, участвующем в передаче мощности от ведущего шкива к ведомому, в ремне возникают еще два вида дополнительных напряжений – изгибные и центробежные.

Изгибные напряжения возникают при изгибе ремня в момент огибания им шкивов, при этом наибольшая величина изгибных напряжений соответствует меньшему радиусу изгиба, то есть максимальные напряжения изгиба возникают в ремне при обегании меньшего (чаще всего являющегося ведущим) шкива. Учитывая последнее, на основе формул сопротивления мате­риалов получаем

, (2.26)

Таблица 2.3. Модуль упругости материала некоторых ремней Тип ремня Модуль упругостиE, МПа Резинотканевый 200…300 Капроновый Клиновой: кордтканевый кордшнуровой 250…400 500…600

где E – модуль упругости материала ремня (см. табл. 2.3), y₀ – расстояние от нейтрального слоя до наружного (растянутого) волокна ремня, D₁ – диаметр наименьшего шкива передачи. Принимая для плоского рем­ня y₀ = d / 2, где d - толщина ремня, а для клинового - y₀ = (0,25…0,38)h, где h – толщина ремня, получаем:

для плоского ремня

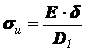, (2.27)

а для клинового ремня

. (2.28)

Таким образом, напряжения изгиба пропорциональны толщине ремня и обратнопропорциональны диаметру наименьшего из шкивов, работающих в передаче.

Часть ремня, прилегающая к шкиву участвует в круговом движении, что обусловливает действие на неё центробежных сил, вызывающих в ремне растягивающие напряжения. Напряжения от центробежных сил можно вычислить по простому соотношению

, (2.29)

где r - средняя плотность материала ремня, а V_р – средняя скорость движения ремня, обегающего шкив.

Выражая скорость ремня через частоту вращения и диаметр наименьшего шкива, получим

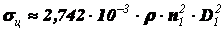. (2.30)

Как видим, напряжения, вызванные в ремне действием центробежных сил, квадратично зависят как от частоты вращения наименьшего шкива, так и от его диаметра.

На внешней стороне ремня все три вида названных напряжений являются растягивающими и потому суммируются. Таким образом, максимальные растягивающие напряжения в ремне

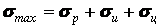. (2.31)

Анализ реальных передач показывает, что напряжения от изгиба s_и и от действия центробежных сил s_ц обычно сравнимы и часто даже превосходят по величине напряжения от рабочей нагрузки s_р. При этом следует учитывать, что увеличение s_и не способствует повышению тяговой способности передачи, с другой стороны, эти напряжения, периодически меняясь, являются главной причиной усталостного износа ремней.

Расчет ременных передач основан на общей теории ременных передач и экспериментальных данных. При этом формула Эйлера и зависимость (2.31) непосредственно не используются, а влияние дополнительных напряжений s_и и s_ц на долговечность передачи учитывают при выборе её геометрических параметров (a, D₁, a и др.) и допускаемых напряжений [s_t]₀ и [s_t], используемых в расчете.

При проектном расчете диаметр малого шкива D₁ можно оценить по модифицированной формуле М.А. Саверина

Таблица 2.4 Коэффициент KD для некоторых передач Тип передачи KD,мм Плоскоременная 55…65 Клиноременная 30…40 Клиноременная, узкий ремень 20…25 Поликлиноременная 25…30

, (2.32)

где вращающий момент T₁ в Нм, диаметр малого шкива D₁ в мм, а эмпирический коэффициент K_D для различных типов передач представлен в табл. 2.4. Получен­ный расчетом диаметр малого шкива увеличивается до ближайшего большего стандартного ли­нейного размера.

Далее расчет плоскоременной передачи базируется на показателях тяговой способности и сводится к выполнению основного условия прочности ремня

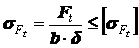; (2.33)

где F_t – окружная сила, передаваемая ремнем, Н; s_Ft – расчетное полезное напряжение, МПа; b и d - ширина и толщина ремня, мм. При этом допускаемое полезное напряжение определяется исходя из опытных данных, полученных при стандартном испытании ремня, с введением поправок на пространственное расположение передачи, угол обхвата на малом шкиве и скорость движения ремня (уменьшение сцепления центробежными силами), на режим работы передачи.

Обычно такой расчет предполагает минимальный срок службы передачи (ремня) 2000 ч. Однако, экспериментально установлено, что для ремней не удается установить предел неограниченной выносливости, а ресурс ремня, выраженный числом пробегов за срок службыN, связан с наибольшим напряжением, вычисленным по зависимости (2.31), соотношением

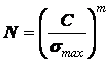. (2.34)

Вводя в рассмотрение число пробегов ремня в секунду 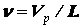при постоянном режиме нагружения и u » 1 (a = 180°), нетрудно получить выражение для определения срока службы ремня T₀ в часах работы

, (2.35)

где z_ш – число шкивов, огибаемых ремнем. Формулы (2.34) и (2.35) получены при диаметре малого шкива D₁ = 200 мм, u » 1 (угол охвата малого шкива a = 180°) и s₀ = 1,2 МПа. Опытные значения коэффициентов C и m для некоторых типов ремней представлены в табл. 2.5.

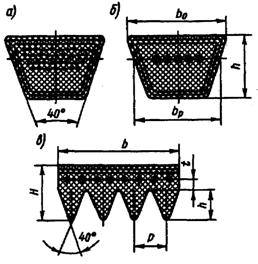Рис. 2.5. Размеры сечений клинового (а, б) и поликлинового(в) ремней

Таблица 2.5 Коэффициенты C и m для некоторых типов ремней Тип ремня C, МПа m Плоский прорезиненный 60…70 5…6 Клиновой:     кордтканевый 9…11 кордшнуровой 6…11

 

Особенности конструкции, работы и расчета клиноременных и поликлиноременных передач.Клиновые ремни имеют трапециевидное поперечное сечение, а поликлиновые – выполненную в форме сочленённых основаниями клиньев рабочую часть (рис. 2.5). Угол клина для обоих видов ремней одинаков и составляет 40°. На шкивах такой передачи выполняются соответствующие сечению рабочей части ремня канавки, называемые ручьями. Профили ремней и ручьёв шкивов контактируют только боковыми (рабочими) поверхностями (рис. 2.6). В клиноременных передачах для снижения изгибных напряжений часто применяют комплект из нескольких ремней (2…6), работающих параллельно на одной паре шкивов. Размеры сечений клиновых ремней стандартизованы (ГОСТ 1284.1-89, ГОСТ 1284.2-89, ГОСТ 1284.3-89). Стандартом предусмотрено 7 ремней нормального сечения (Z, A, B, C, D, E, E0), у которых b₀/h»1,6, и 4 – узкого сечения (YZ, YA, YB, YC), у которых b₀/h»1,25. Ремни изготавливаются в виде замкнутого кольца, поэтому их длина тоже стандартизована.

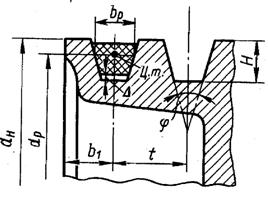Рис. 2.6. Расположение клинового ремня в ручье шкива.

Таким образом, ремень со шкивом образуют клиновую кинематическую пару, для которой приведенный коэффициент трения f* выражается зависимостью

, (2.36)

где f – коэффициент трения между контактирующими поверхностями ремня и шкива, а j - угол между боковыми рабочими поверхностями ремня. После подстановки в (2.36) фактического значения угла j получаем, что f*=2,92 f, то есть при одном и том же диаметре ведущего шкива несущая способность клиноременной передачи будет примерно втрое выше по сравнению с плоскоременной. Поэтому, если в плоскоременных передачах рекомендуют угол охвата меньшего шкива a ³ 150°, то в клиноременных - a ³ 120° и допускается даже a = 75…80°. Последнее обстоятельство позволяет использовать 1 ремень для передачи вращательного движения от одного ведущего нескольким ведомым шкивам (например, в автомобильных ДВС используется ременный привод одним ремнем водяной помпы в системе охлаждения, электрогенератора и вентилятора).

Проектный расчет клиноременных передач выполняется достаточно просто методом подбора, поскольку в стандартах указывается мощность, передаваемая одним ремнем при определенном расчетном диаметре меньшего шкива и известной средней скорости ремня или частоте вращения шкива.

Изложенная лекция, как и предыдущая, состоит из двух частей, первая из которых посвящена общим вопросам проектирования механических передач. В этой части лекции представлены основные параметры, характеризующие всякую механическую передачу, и показана связь между ними.

Во второй части лекции изложены теоретические основы расчета ременных передач, их геометрические, кинематические и силовые характеристики, представлены соотношения связывающие различные параметры ременных передач между собой. Более полные сведения о ременных передачах можно найти в учебной и технической литературе.

Вопросы для самоконтроля:

1. Какое устройство можно назвать механической передачей?

2. Какие основные параметры характеризуют механическую передачу?

3. В чем заключается разница между передаточным отношением и передаточным числом?

4. Что означает коэффициент полезного действия, коэффициент потерь, какова их сумма?

5. В чем разница между угловой скоростью и частотой вращения, в каких единицах они измеряются?

6. Как связаны скоростные и нагрузочные параметры прямолинейного и вращательного движения?

7. Как связаны тангенциальная сила и вращающий момент, ею создаваемый?

8. Что называют ременной передачей?

9. Какие виды ремней используются в ременных передачах?

10. Назовите основные геометрические параметры ременной передачи.

11. Каковы соотношения между силами натяжения ветвей ремня в ременной передаче - при неработающей передаче, в процессе работы?

12. Что характеризует коэффициент тяги ременной передачи?

13. Какие показатели ременной передачи непосредственно влияют на величину оптимального коэффициента тяги?

14. Что характеризует коэффициент скольжения ременной передачи?

15. Как определить точное значение передаточного числа ременной передачи?

16. Как меняется коэффициент скольжения и КПД с ростом коэффициента тяги?

17. Какие силы создают напряжения в ремне при работе ременной передачи?

18. Какие процессы, происходящие в ремне при работе передачи, ответственны за его усталостный износ?

19. Как выполняется проектный расчет плоскоременной передачи?

20. По какому критерию выполняется проверочный расчет ременной передачи?

21. Назовите основные особенности поперечного сечения клинового и поликлинового ремней?

22. Почему передача клиновым ремнем имеет большую несущую способность по сравнению с плоскоременной?

23. По каким критериям выполняется проектный расчет клиноременной передачи?

 

 

é