Основные показатели среднего уровня вариационного ряда (средняя арифметическая; мода; медиана)

 

При изучении особенностей статистического распределения, прежде всего, следует найти его центральное значение, т.е. средний уровень. Для характеристики центра распределения применяются показатели, получившие название средних величин.

Самый распространенный вид средних – средняя арифметическая: простая или взвешенная.

Средняя арифметическая простая (невзвешенная) равна сумме отдельных значений признака, деленной на число этих значений.

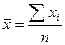- средняя арифметическая простая.

Простая средняя арифметическая применяется в случаях, когда имеются отдельные значения признака, т.е. данные не сгруппированы. Если данные представлены в виде рядов распределения или группировок, то средняя исчисляется иначе.

- средняя арифметическая взвешенная.

В формулах средней арифметической взвешенной, рассчитываемой для интервального вариационного ряда, в качестве х_i принято брать середину интервала.

Средняя арифметическая обладает рядом свойств:

1. От уменьшения или увеличения частот каждого значения признака х_i в n раз величина средней арифметической не изменится.

Если все частоты разделить или умножить на какое-либо число, то величина средней не изменится.

2. Общий множитель индивидуальных значений признака может быть вынесен за знак средней:

3. Средняя суммы (разности) двух или нескольких величин равна сумме (разности) их средних:

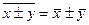
4. Если х = с, где с - постоянная величина, то .

5. Сумма отклонений значений признака х_i от средней арифметической х равна нулю.

При изучении вариации применяются такие характеристики вариационного ряда, которые описывают количественно его структуру, строение. Такова, например, медиана- величина варьирующего признака, делящая совокупность на две равные части ~ со значениями признака меньше медианы и со значениями признака больше медианы.

Медиана не зависит от значений признака на краях ранжированного ряда. Поэтому часто медиану используют как более надежный показатель типичного значения признака, нежели арифметическая средняя, если ряд значений неоднороден, включает резкие отклонения от средней.

При четном числе единиц совокупности за медиану принимают арифметическую среднюю величину из двух центральных вариант, например при десяти значениях признака - среднюю из пятого и шестого значений в ранжированном ряду.

В интервальном вариационном ряду для нахождения медианы применяется формула

,

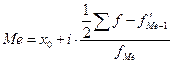где х₀ - нижняя граница медианного интервала;

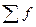- сумма частот;

- накопленная частота интервала, предшествующего медианному

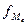- частота медианного интервала.

Значимой является такая величина признака, которая встречается в изучаемом ряду, в совокупности чаще всего. Такую величину принято называть модой и обозначать Мо. В дискретном ряду мода определяется без вычисления как значение признака с наибольшей частотой. Обычно встречаются ряды с одним модальным значением признака. Если два или несколько равных (и даже несколько различных, но больших, чем соседние) значений признака имеются в вариационном ряду, он считается соответственно бимодальным («верблюдообразным») либо мультимодальным. Это говорит о неоднородности совокупности, возможно, представляющей собой агрегат нескольких совокупностей с разными модами.

В интервальном вариационном ряду, тем более при непрерывной вариации признака, строго говоря, каждое значение признака встречается только один раз. Модальным интервалом является интервал с наибольшей частотой. Внутри этого интервала находят условное значение признака, вблизи которого плотность распределения, т.е. число единиц совокупности, приходящееся на единицу измерения варьирующего признака, достигает максимума. Это условное значение и считается точечной модой. Логично предположить, что такая точечная мода располагается ближе к той из границ интервала, за которой частота в соседнем интервале больше частоты в интервале за другой границей модального интервала. Отсюда имеем обычно применяемую формулу

,

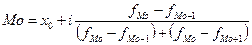где х₀ - нижняя граница модального интервала;

i - величина модального интервала;

- частота модального интервала;

- частота интервала, предшествующего модальному;

- частота интервала, следующего за модальным.

Если распределение по форме близко к нормальному закону, то медиана находится между модой и средней величиной, причем ближе к средней, чем к моде.

При правосторонней асимметриих̅ > Me > Mo;

при левосторонней асимметрии х̅ < Me < Mo.

Для умеренно асимметричных распределений справедливо равенство:

 

Показатели вариации и способы их расчета (среднее линейное отклонение; дисперсия; межгрупповая и внутригрупповая дисперсии; коэффициент детерминации и эмпирическое корреляционное отношение; правило сложения дисперсий для доли признака; среднее квадратическое отклонение, показатели относительного рассеивания)

Средняя величина — это абстрактная, обобщающая характеристика признака изучаемой совокупности, но она не показывает строения совокупности, которое весьма существенно для ее познания. Средняя величина не дает представления о том, каким образом отдельные значения изучаемого признака группируются вокруг средней, сосредоточены ли они вблизи или значительно отклоняются от нее. В некоторых случаях отдельные значения признака близко примыкают к средней арифметической и мало от нее отличаются. В таких случаях средняя хорошо представляет всю совокупность. В других, наоборот, отдельные значения совокупности далеко отстают от средней, и средняя плохо представляет всю совокупность.

Колеблемость отдельных значений признака характеризуют показатели вариации.

Анализ систематической вариации позволяет оценить степень зависимости изменений в изучаемом признаке от определяющих ее факторов. Например, изучая силу и характер вариации в выделяемой совокупности, можно оценить, насколько однородной является данная совокупность в количественном, а иногда и качественном отношении, а, следовательно, насколько характерной является исчисленная средняя величина. Степень близости данных отдельных единиц х_i к средней измеряется рядом абсолютных, средних и относительных показателей.

Наиболее простой показатель вариации - размах вариации.

Размах вариации - это разность между наибольшим ( 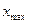) и наименьшим ( ) значениями вариантов:

.