Многозвенные зубчатые механизмы с подвижными осями (эпициклические). Определение их передаточного отношения, область применения

Эпициклическим называется механизм, имеющий в своем составе хотя бы одно звено с подвижной геометрической осью в пространстве.

Звено, имеющее подвижную геометрическую ось в пространстве, называется сателлит. Звено, на которое устанавливают ось сателлитов, называется водилом. Звено водила принято обозначать не цифрой, а латинской буквой h. Зубчатые колеса, имеющие неподвижную геометрическую ось в пространстве, называются центральными. Центральное колесо, имеющее внешние зубья, называется солнечное колесо. Центральное колесо, имеющие внутренние зубья, называется коронная шестерня (опорное колесо).

Достоинства эпициклических передач:

- компактность при больших передаточных отношениях;

- возможность передачи больших крутящих моментов (при их передаче используется несколько сателлитов, на одной планетарной передаче можно поставить до 24 сателлитов).

- очень высокий КПД, в среднем 0,99.

Недостатки:

- сложность изготовления;

- высокая точность изготовления и сборки

- если число сателлитов неравно 3, то необходим специальный механизм, который бы выравнивал нагрузку между сателлитами. Этот механизм утяжеляет и удорожает конструкцию.

 

Планетарные механизмы

Сложные зубчатые механизмы, в которых ось хотя бы одного колеса подвижна, а одно из центральных зубчатых колес неподвижно, называются планетарными механизмами.

Рис. 3.7. Планетарная передача: 1 – центральное колесо; 2 – сателлиты; 3 – опорное (неподвижное) колесо; h – водило (от заглавной буквы слова hedel – рычаг)

Используем метод обращения движения, когда всему механизму, в том числе неподвижному колесу, условно придается (сообщается) угловая скорость (т.е. все звенья в таком механизме уменьшают скорость на величину угловой скорости водила ). Тогда в этом так называемом обращенном механизме водило H станет неподвижным, и мы получим простой ступенчатый механизм с неподвижными осями. Угловые скорости исходного планетарного и обращенного механизма сведем в таблицу 3.1:

Таблица 3.1

№ звеньев	Угловые скорости в механизме
планетарном	обращенном
H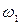

 

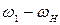
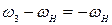
Вычисляем передаточные отношения обращенного механизма (на примере схемы 1):

через угловые скорости:

;

через числа зубьев колес:

.

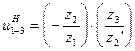Окончательно получим .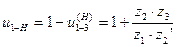

Для других схем планетарных механизмов (см. табл. 3.2) выводы формул расчета передаточных отношений аналогичны предыдущему.

Общая формула имеет вид

,

где – передаточное отношение обращенного механизма.

Передаточное отношение планетарного механизма от подвижного центрального колеса 1 к водилу Н при неподвижном колесе 3 равно единица минус передаточное отношение обращенного механизма от подвижного центрального колеса к неподвижному колесу 3 при неподвижном водиле Н.

Основные типы планетарных передач, их КПД, формулы для расчета и возможные значения передаточных отношений приведены в табл. 3.2

Таблица 3.2

Типовые планетарные механизмы