Общие понятия и классификация фильтров.
На современном этапе развития радиотехники и радиоэлектроники многие схемные решения, ранее применявшиеся повсеместно, претерпели коренной пересмотр из-за широкого внедрения микроэлектронных устройств. В значительной степени это коснулось теории и практики построения частотно-избирательных фильтров.
Было выяснено, что создать катушку индуктивности в микроэлектронном исполнении практически невозможно. Однако, для реализации обычных колебательных звеньев 2-го порядка необходимо располагать индуктивными элементами. Выходом из этого положения явилась разработка так называемых активных RС-фильтров. Они представляют собой комбинации пассивных RС-цепей и активных элементов, как правило, сложных транзисторных устройств, которые передают в пассивные цепи некоторую мощность от источника питания.
В этом разделе будет рассмотрен один из возможных принципов построения активных RС-фильтров, когда в качестве активного элемента используется операционный усилитель.
Среди преимуществ активных фильтров по сравнению с пассивными следует выделить:
· отсутствие катушек индуктивности;
· лучшая избирательность;
· компенсация затухания полезных сигналов или даже их усиление;
· пригодность к реализации в виде ИМС.
Активные фильтры имеют и недостатки:
- потребление энергии от источника питания;
- ограниченный динамический диапазон;
- дополнительные нелинейные искажения сигнала.
Отметим так же, что использование активных фильтров с ОУ на частотах свыше десятков мегагерц затруднено из-за малой частоты единичного усиления fT большинства ОУ широкого применения. Особенно преимущество активных фильтров на ОУ проявляется на самых низких частотах, вплоть до долей герц.
В активных фильтрах обеспечивается получение АЧХ всех разновидностей фильтров: нижних частот (ФНЧ), верхних частот (ФВЧ), полосовых (ПФ) и режекторных (РФ).
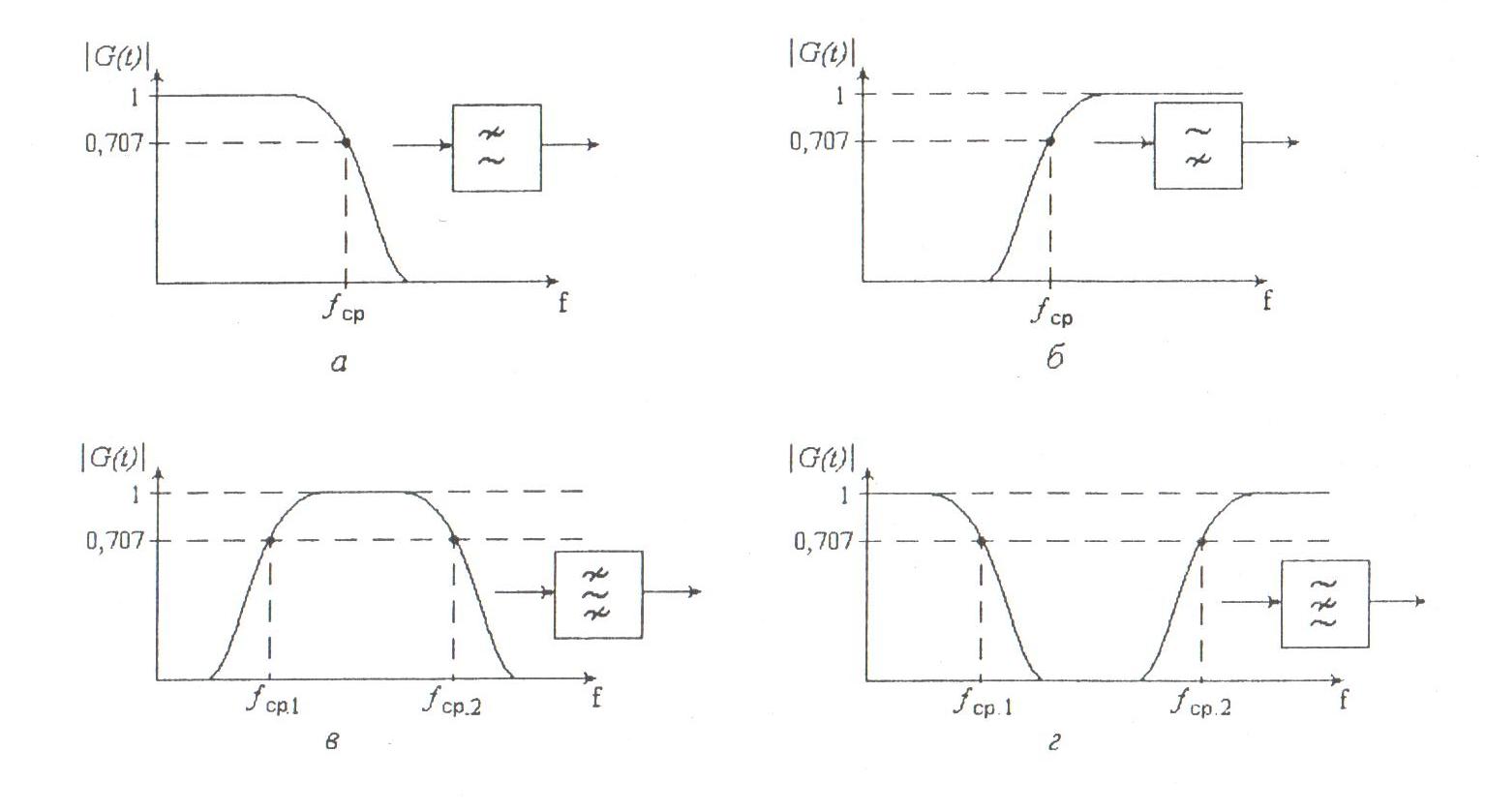
Рисунок 7.4. Классификация фильтров по виду АЧХ
Операторная передаточная функция активного фильтра, так же , как и пассивного представляет собой отношение двух полиномов:
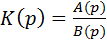
и однозначно определяется нулями и полюсами. Простейший полином числителя — константа. Такие фильтры называются полиномиальными.
Число полюсов функции (а в активных фильтрах на ОУ число полюсов обычно равно числу конденсаторов в цепях, формирующих АЧХ) определяет порядок фильтра. Порядок фильтра указывает на скорость спада его АЧХ, которая для первого порядка составляет 20дБ/дек, для второго — 40дБ/дек, для третьего — 60дБ/дек и т.д.
. В большинстве случаев задают АЧХ, принимая нормированный коэффициент передачи:
 , (7.2)
, (7.2)
где 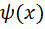 - функция фильтрации;
- функция фильтрации; 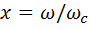 — нормированная частота;
— нормированная частота; 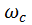 - частота среза фильтра; ε - допустимая неравномерность АЧХ в полосе пропускания.
- частота среза фильтра; ε - допустимая неравномерность АЧХ в полосе пропускания.
В зависимости от того, какая функция принимается в качестве 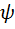
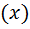 различают фильтры Баттерворта, Чебышева, Кауэра, Золотарёва, Бесселя и др. На рисунке 7.4 в качестве примера приведены АЧХ фильтров НЧ Баттерворта и Чебышева различных порядков.
различают фильтры Баттерворта, Чебышева, Кауэра, Золотарёва, Бесселя и др. На рисунке 7.4 в качестве примера приведены АЧХ фильтров НЧ Баттерворта и Чебышева различных порядков.
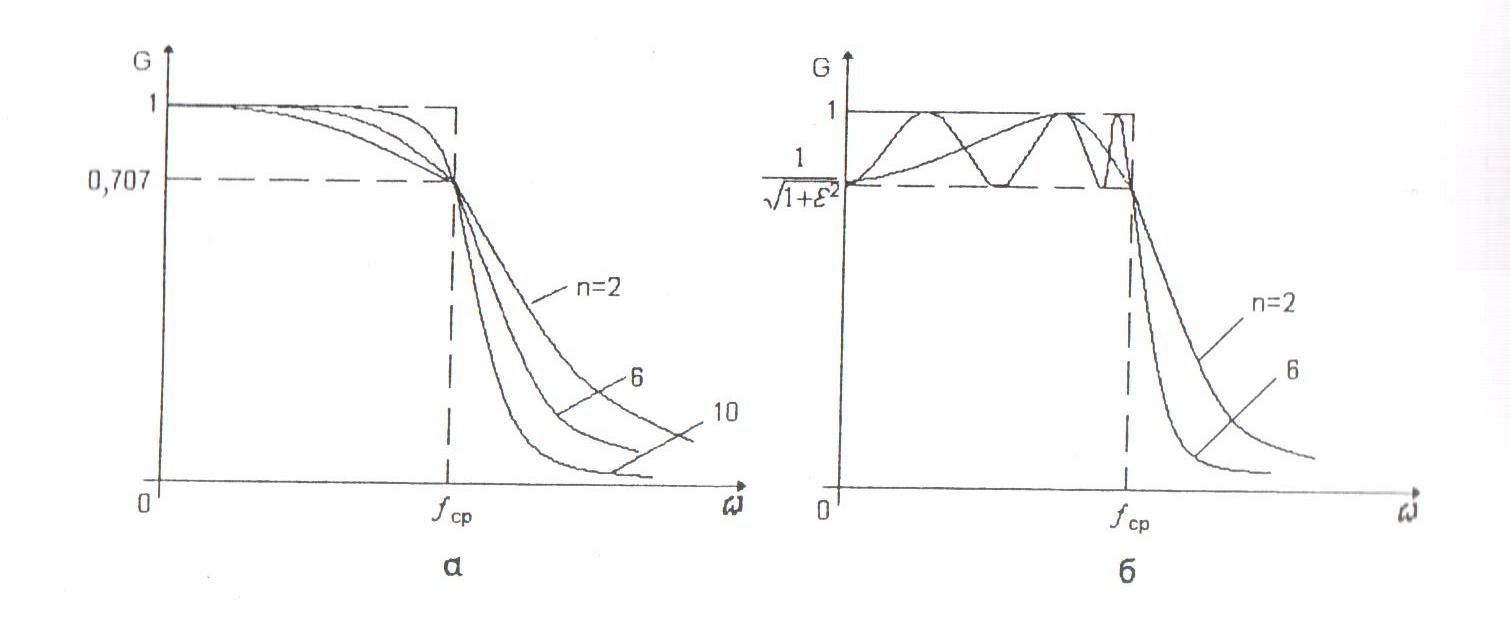
Рисунок 7.5. АЧХ фильтров НЧ Баттерворта (а) и Чебышева (б) различных порядков.
Фильтр Баттерворта описывает АЧХ с максимально плоской частью в полосе пропускания и относительно небольшой скоростью спада. Фильтр Чебышева описывает АЧХ с определенной неравномерностью в полосе пропускания, но с большей скоростью спада. .
Помимо перечисленных аппроксимаций АЧХ активных фильтров известны и другие, например, обратного фильтра Чебышева, фильтра Золотарева и т.д.
Существует множество способов схемотехнической реализации АRC- фильтров. Заметим, что схемы активных фильтров не изменяются в зависимости от типа аппроксимации АЧХ, а лишь изменяются соотношения между их элементами. Рассмотрим наиболее часто применяемые на практике варианты построения АRC- фильтров на основе ОУ.
Схемы простейших (первого порядка) ФВЧ, ФНЧ, ПФ и их логарифмические АЧХ приведены на рисунке 7.6. В этих фильтрах конденсатор, определяющий частотную характеристику, включен в цепь ООС.
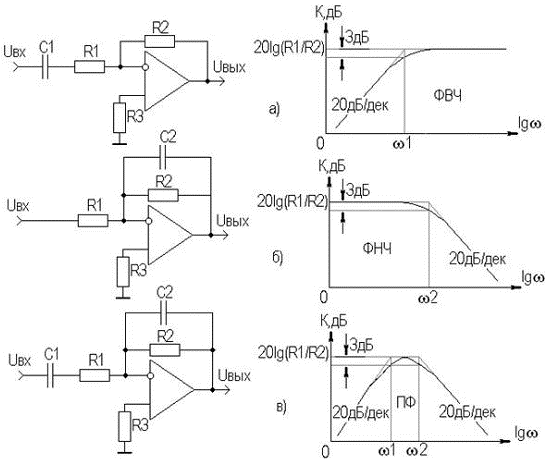
Рисунок 7.6. Простейшие активные фильтры:
а) - ФВЧ, б) – ФНЧ, в) – ПФ
Для ФВЧ (рисунок 7.6, а) комплексный коэффициент передачи равен:
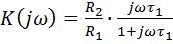 ,
,
где τ1=C1R1.
Частоту сопряжения асимптот ω1 находят из условия ω1τ1=1, откуда
f1 = 1/2πτ1.
Для ФНЧ (рисунок 7.6,б) имеем:
 ,
,
где τ2=C2R2, f2 = 1/2πτ2.
В ПФ (рисунок 7.6, в) присутствуют элементы ФВЧ и ФНЧ.
Можно увеличить крутизну спада ЛАЧХ, если увеличить порядок фильтров. Активные ФНЧ, ФВЧ и ПФ второго порядка приведены на рисунке 7.6 . Наклон асимптот у них может достигать 40дБ/дек, а переход от ФНЧ к ФВЧ, как видно из рисунков 7.6,а,б осуществляется заменой резисторов на конденсаторы, и наоборот. В ПФ (рисунок 7.6,в) имеются элементы ФВЧ и ФНЧ. Передаточные функции равны:
- для ФНЧ:
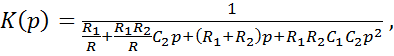
- для ФВЧ:
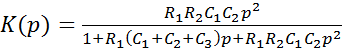 .
.
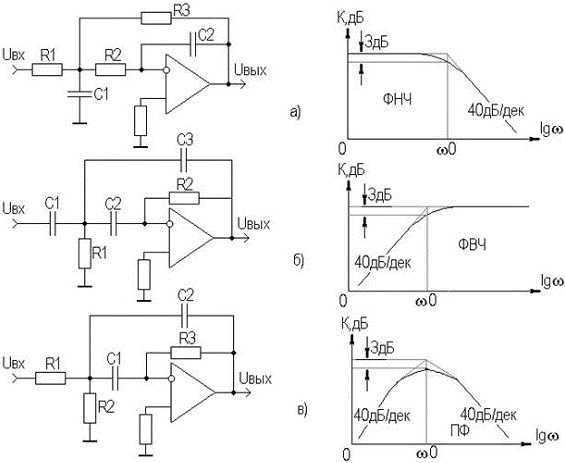
Рисунок 7. 6.-Активные фильтры второго порядка с многопетлевой ОС:
а) - ФНЧ, б) – ФВЧ, в) – ПФ.
- для ПФ:
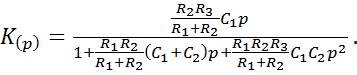
Резонансная частота равна:
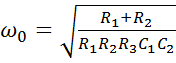 .
.
Для ФНЧ и ФВЧ частоты среза соответственно равны:
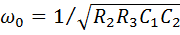 ;
; 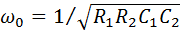 .
.
Достоинством рассмотренных схем фильтров с многопетлевой ОС является возможность получения высоких коэффициентов усиления, низкое выходное сопротивление и относительная простота настройки.
Кроме указанных схем существуют и другие варианты построения.
Следует отметить, что проектирование фильтров в настоящее время автоматизировано и процедура их проектирования включена во многие программные комплексы для схемотехнического моделирования и проектирования.
Контрольные вопросы
1. Назначение и области применения избирательных усилителей.
2. Основные параметры и характеристики избирательных усилителей.
3. Избирательный усилитель с 2Т-мостом, параметры и характеристики.
4. Факторы, влияющие на добротность избирательного усилителя с 2Т-мостом.
5. Достоинства и недостатки избирательного усилителя с 2Т-мостом.
6. Избирательный усилитель с мостом Вина.
7. Достоинства и недостатки избирательного усилителя с мостом Вина.
8. Классификация и основные параметры фильтров.
9. Преимущества активных фильтров перед пассивными.
10. Особенности схемотехнической реализации ФНЧ и ФВЧ.