Аксиомы вероятности (аксиомы Колмогорова)

 

· Аксиома №1 (аксиома неотрицательности):

Р(А)³0 , для любого АÎE или АÎF

Каждому событию А соответствует неотрицательное число – вероятность этого события.

· Аксиома №2 (аксиома нормировки):

Р(W)=1.

Вероятность достоверного события равна 1.

· Аксиома №3 (аксиома аддитивности):

Если заданы события 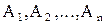такие, что 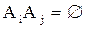при i¹j, то

(*)

Вероятность суммы несовместных событий равна сумме вероятностей.

Замечание: Функции множеств, обладающие свойством (*) при n< называются аддитивными мерами, а при n= – счетно-аддитивными мерами.

Определение:Вероятность – неотрицательная, нормированная к единице мера, заданная на измеримом пространстве событий, характеризующая степень возможности появления событий.

Соответствие между событиями и их вероятностями называется распределением вероятности.

Таким образом, Р(А), как функция множествАÎF, (E) определяет распределение вероятностей на F,(E). Пространство элементарных событий W с заданной на нем алгеброй E (или s-алгеброй F) подмножеств и определенной на E(F) вероятностью Р называется вероятностным пространством.

Обозначение вероятностного пространства: (W,E,Р) или (W,F,Р). Вероятностное пространство определяет вероятностную модель рассматриваемого случайного явления.